
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,OD⊥BC于E. 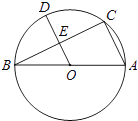
(1)求证:OD∥AC;
(2)若BC=8,DE=3,求⊙O的直径.
【答案】
(1)证明:∵AB是⊙O的直径,∴∠C=90°,
∵OD⊥BC,∴∠OEB=∠C=90°,
∴OD∥AC
(2)解:令⊙O的半径为r,
根据垂径定理可得:BE=CE= ![]() BC=4,
BC=4,
由勾股定理得:r2=42+(r﹣3)2,
解得:r= ![]() ,
,
所以⊙O的直径为 ![]()
【解析】(1)由圆周角定理得出∠C=90°,再由垂径定理得出∠OEB=∠C=90°,即可得出结论;(2)令⊙O的半径为r,由垂径定理得出BE=CE= ![]() BC=4,由勾股定理得出方程,解方程求出半径,即可得出⊙O的直径.
BC=4,由勾股定理得出方程,解方程求出半径,即可得出⊙O的直径.
【考点精析】本题主要考查了勾股定理的概念和垂径定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图,其中每个小正方形的边长为1个单位长度.
(1)按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点C顺时针旋转90°得到△A2B2C2.
(2)回答下列问题:
①△A1B1C1中顶点A1坐标为 ;
②若P(a,b)为△ABC边上一点,则按照(1)中①作图,点P对应的点P1的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)-16+23+(-17)-(-7)
(2) ![]()
(3)![]()
(4)(-8)÷(![]() )-2×(-6)
)-2×(-6)
(5)![]()
(6)(-![]() )2×
)2×![]() ÷|-
÷|-![]() |+(-2)÷(
|+(-2)÷(![]() )4
)4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An﹣1An(n为正整数),过A1 , A2 , A3 , …,An分别作x轴的平行线,与反比例函数y= ![]() (x>0)交于点B1 , B2 , B3 , …,Bn , 如图所示的Rt△B1C1B2 , Rt△B2C2B3 , Rt△B3C3B4 , …,Rt△Bn﹣1Cn﹣1Bn面积分别记为S1 , S2 , S3 , …,Sn﹣1 , 则S1+S2+S3+…+Sn﹣1=( )
(x>0)交于点B1 , B2 , B3 , …,Bn , 如图所示的Rt△B1C1B2 , Rt△B2C2B3 , Rt△B3C3B4 , …,Rt△Bn﹣1Cn﹣1Bn面积分别记为S1 , S2 , S3 , …,Sn﹣1 , 则S1+S2+S3+…+Sn﹣1=( ) 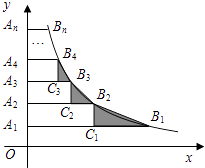
A.1
B.2
C.1﹣ ![]()
D.2﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架长2.5m的梯子AB斜靠在墙AC上,∠C=90°,此时,梯子的底端B离墙底C的距离BC为0.7m.
(1)求此时梯子的顶端A距地面的高度AC;
(2)如果梯子的顶端A下滑了0.9m,那么梯子的顶端B在水平方向上向右滑动了多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=kx+b和函数y=ax+m的图像如图所示,求下列不等式(组)的解集
(1) kx+b <ax+m的解集是
(2)![]() 的解集是
的解集是
(3)![]() 的解集是
的解集是
(4)![]() 的解集是
的解集是
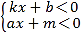
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆分别与AB、AC边相切于D、E两点,连接OD.已知BD=2,AD=3. 
求:
(1)tanC;
(2)图中两部分阴影面积的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B在数轴上表示的数分别为m、n.
(1)对照数轴完成下表:

(2)若A、B两点间的距离为d,试写出d与m、n之间数量关系,并用文字语言描述
这个数量关系;
(3)已知A、B两点在数轴上表示的数分别为x和-2,则A、B两点的距离d可表示
为 ;如果d=3,求x的值。
(4)若数轴上表示数m的点位于表示数-5和3的点之间,求|m+5|+|m-3|的值(用含x的式子表示);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com