
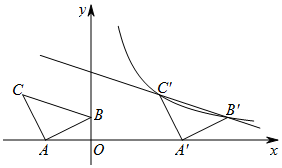
 如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).
如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).分析 (1)作CN⊥x轴于点N,根据HL证明Rt△CAN≌Rt△AOB,求出NO的长度,进而求出d;
(2)设△ABC沿x轴的正方向平移c个单位,用c表示出C′和B′,根据两点都在反比例函数图象上,求出k的值,进而求出c的值,即可求出反比例函数和直线B′C′的解析式;
(3)直接从图象上找出y1<y2时,x的取值范围.
解答 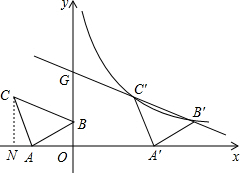 解:(1)作CN⊥x轴于点N,
解:(1)作CN⊥x轴于点N,
∵A(-2,0)B(0,1).
∴OB=1,AO=2,
在Rt△CAN和Rt△AOB,
∵$\left\{\begin{array}{l}{CN=AO}\\{AC=AB}\end{array}\right.$,
∴Rt△CAN≌Rt△AOB(HL),
∴AN=BO=1,CN=AO=2,NO=NA+AO=3,
又∵点C在第二象限,
∴C(-3,2);
(2)设△ABC沿x轴的正方向平移c个单位,
则C′(-3+c,2),则B′(c,1)
又点C′和B′在该比例函数图象上,
把点C′和B′的坐标分别代入y1=$\frac{k}{x}$,
得-6+2c=c,
解得c=6,
即反比例函数解析式为y1=$\frac{6}{x}$,
(3)此时 C′(3,2),B′(6,1),
设直线B′C′的解析式y2=mx+n,
∵$\left\{\begin{array}{l}{2=3m+n}\\{1=6m+n}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m=-\frac{1}{3}}\\{n=3}\\{\;}\end{array}\right.$,
∴直线C′B′的解析式为y2=-$\frac{1}{3}$x+3;
由图象可知反比例函数y1和此时的直线B′C′的交点为 C′(3,2),B′(6,1),
∴若y1<y2时,则3<x<6.
点评 本题主要考查了反比例函数的综合题的知识,解答本题的关键是熟练掌握反比例函数的性质以及平移的知识,解决第(2)问关键求出c的值,此题难度不是很大.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:选择题
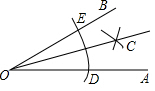 在数学课上,老师用直尺和圆规作角平分线,方法如下:
在数学课上,老师用直尺和圆规作角平分线,方法如下:| A. | SAS | B. | ASA | C. | SSS | D. | AAS |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知A,E,F,C在同一条直线上,∠A=∠C,AE=CF,要使△ADF≌△CBE,还需要添加一个条件,这个条件可以是AD=BC(只需写出一个)
如图,已知A,E,F,C在同一条直线上,∠A=∠C,AE=CF,要使△ADF≌△CBE,还需要添加一个条件,这个条件可以是AD=BC(只需写出一个)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 361×106 | B. | 36.1×107 | C. | 3.61×108 | D. | 0.361×109 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com