
”¾ĢāÄæ”æŅŃÖŖČēĶ¼£¬Å×ĪļĻßy=![]() x2+
x2+![]() x©
x©![]() ÓėxÖį½»ÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄ×ó²ą£©ÓėyÖį½»ÓŚµćC£¬Ö±ĻßBE”ĶBCÓėµćB£¬ÓėÅ×ĪļĻßµÄĮķŅ»½»µćĪŖE£®
ÓėxÖį½»ÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄ×ó²ą£©ÓėyÖį½»ÓŚµćC£¬Ö±ĻßBE”ĶBCÓėµćB£¬ÓėÅ×ĪļĻßµÄĮķŅ»½»µćĪŖE£®
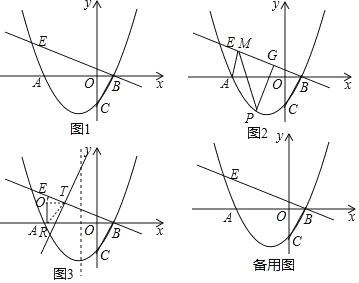
£Ø1£©ČēĶ¼1£¬ĒóµćEµÄ×ų±ź£»
£Ø2£©ČēĶ¼2£¬ČōµćPĪŖxÖįĻĀ·½Å×ĪļĻßÉĻŅ»¶Æµć£¬¹żP×÷PG”ĶBEÓėµćG£¬µ±PG³¤¶Č×ī“óŹ±£¬ŌŚÖ±ĻßBEÉĻÕŅŅ»µćM£¬Ź¹µĆ”÷APMµÄÖܳ¤×īŠ”£¬²¢Ēó³öÖܳ¤µÄ×īŠ”Öµ£®
£Ø3£©ČēĶ¼3£¬½«”÷BOCŌŚÉäĻßBEÉĻ£¬ÉčĘ½ŅĘŗóµÄČż½ĒŠĪĪŖ”÷B”äO”äC”䣬B”äŌŚÉäĻßBEÉĻ£¬ČōÖ±ĻßB”äC”ä·Ö±šÓėxÖį”¢Å×ĪļĻߵĶŌ³ĘÖį½»ÓŚµćR”¢T£¬µ±”÷O”äRTĪŖµČŃüČż½ĒŠĪŹ±£¬ĒóRµÄ×ų±ź£®
”¾“š°ø”æ£Ø1£©E£Ø©4£¬![]() £©£»£Ø2£©
£©£»£Ø2£©![]() £»£Ø3£©R£Ø
£»£Ø3£©R£Ø![]() £¬0£©»ņ£Ø
£¬0£©»ņ£Ø![]() £¬0£©»ņ£Ø
£¬0£©»ņ£Ø![]() £¬0£©»ņ£Ø
£¬0£©»ņ£Ø![]() £¬0£©£®
£¬0£©£®
”¾½āĪö”æ
£Ø1£©Ēó³öÖ±ĻßBEµÄ½āĪöŹ½£¬ĄūÓĆ·½³Ģ×éĒó³ö½»µćE×ų±ź£»
£Ø2£©ČēĶ¼2ÖŠ£¬×÷PK”ĪOC½»BEÓŚK£®ŅņĪŖ”ĻPKBŹĒ¶ØÖµ=60”ć£¬ĶĘ³öµ±PKµÄÖµ×ī“óŹ±£¬PGµÄÖµ×ī“ó£¬ÉčP£Øm£¬![]() m2+
m2+![]() m©
m©![]() £©£¬ŌņK£Øm£¬©
£©£¬ŌņK£Øm£¬©![]() m+
m+![]() £©£¬æɵĆPK=©
£©£¬æɵĆPK=©![]() m2©
m2©![]() m+
m+![]() £¬æÉÖŖµ±m=©
£¬æÉÖŖµ±m=©![]() Ź±£¬PKµÄÖµ×ī“󣬓ĖŹ±P£Ø©
Ź±£¬PKµÄÖµ×ī“󣬓ĖŹ±P£Ø©![]() £¬©
£¬©![]() £©£®ČēĶ¼2©1ÖŠ£¬×÷A¹ŲÓŚBEµÄ¶Ō³ĘµćA”䣬Į¬½ÓPA”ä½»BEÓŚM£¬Į¬½ÓAM”¢AP£¬“ĖŹ±”÷PAMµÄÖܳ¤×īŠ”£»
£©£®ČēĶ¼2©1ÖŠ£¬×÷A¹ŲÓŚBEµÄ¶Ō³ĘµćA”䣬Į¬½ÓPA”ä½»BEÓŚM£¬Į¬½ÓAM”¢AP£¬“ĖŹ±”÷PAMµÄÖܳ¤×īŠ”£»
£Ø3£©ČēĶ¼3ÖŠ£¬ÉčBB”ä=![]() m£¬ŌņBR=2m£¬R£Ø1©2m£¬0£©£¬O”ä£Ø©
m£¬ŌņBR=2m£¬R£Ø1©2m£¬0£©£¬O”ä£Ø©![]() m£¬
m£¬![]() m£©£¬·ÖČżÖÖĒéŠĪ¢Łµ±O”äT=RTŹ±£»¢Śµ±O”äT=O”äRŹ±£»¢Ūµ±RT=RO”䏱£¬·Ö±š¹¹½Ø·½³Ģ¼“æɽā¾öĪŹĢā.
m£©£¬·ÖČżÖÖĒéŠĪ¢Łµ±O”äT=RTŹ±£»¢Śµ±O”äT=O”äRŹ±£»¢Ūµ±RT=RO”䏱£¬·Ö±š¹¹½Ø·½³Ģ¼“æɽā¾öĪŹĢā.
£Ø1£©”ßÅ×ĪļĻßy=![]() x2+
x2+![]() x©
x©![]() ÓėxÖį½»ÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄ×ó²ą£©ÓėyÖį½»ÓŚµćC£¬
ÓėxÖį½»ÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄ×ó²ą£©ÓėyÖį½»ÓŚµćC£¬
Įīy=0£¬µĆµ½![]() x2+
x2+![]() x©
x©![]() =0£¬½āµĆx=©3»ņ1£¬
=0£¬½āµĆx=©3»ņ1£¬
”ąA£Ø©3£¬0£©£¬B£Ø1£¬0£©£¬
Įīx=0£¬µĆµ½y=©![]() £¬
£¬
”ąC£Ø0£¬©![]() £©£¬
£©£¬
”ąÖ±ĻßBCµÄ½āĪöŹ½ĪŖy=![]() x©
x©![]() £¬
£¬
”ßBE”ĶBC£¬
”ąÖ±ĻßBEµÄ½āĪöŹ½ĪŖy=©![]() x+
x+![]() £¬
£¬
ÓÉ £¬½āµĆ
£¬½āµĆ![]() »ņ
»ņ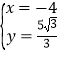 £¬
£¬
”ąE£Ø©4£¬![]() £©£»
£©£»
£Ø2£©ČēĶ¼2ÖŠ£¬×÷PK”ĪOC½»BEÓŚK£®

”ß”ĻPKBŹĒ¶ØÖµ=60”ć£¬
”ąµ±PKµÄÖµ×ī“óŹ±£¬PGµÄÖµ×ī“ó£¬ÉčP£Øm£¬![]() m2+
m2+![]() m©
m©![]() £©£¬ŌņK£Øm£¬©
£©£¬ŌņK£Øm£¬©![]() m+
m+![]() £©£¬
£©£¬
”ąPK=©![]() m2©
m2©![]() m+
m+![]() £¬
£¬
”ß©![]() £¼0£¬
£¼0£¬
”ąµ±m=©![]() Ź±£¬PKµÄÖµ×ī“󣬓ĖŹ±P£Ø©
Ź±£¬PKµÄÖµ×ī“󣬓ĖŹ±P£Ø©![]() £¬©
£¬©![]() £©£®
£©£®
ČēĶ¼2©1ÖŠ£¬×÷A¹ŲÓŚBEµÄ¶Ō³ĘµćA”䣬Į¬½ÓPA”ä½»BEÓŚM£¬Į¬½ÓAM”¢AP£¬“ĖŹ±”÷PAMµÄÖܳ¤×īŠ”£¬
”ßA£Ø©3£¬0£©£¬æɵĆA”ä£Ø©1£¬2![]() £©£¬
£©£¬
”ą”÷PAMµÄÖܳ¤µÄ×īŠ”Öµ=PM+MA+PA=PA+PM+MA”ä=PA+PA”ä=![]() +
+![]() =
=![]() £»
£»
£Ø3£©ČēĶ¼3ÖŠ£¬ÉčBB”ä=![]() m£¬ŌņBR=2m£¬R£Ø1©2m£¬0£©£¬O”ä£Ø©
m£¬ŌņBR=2m£¬R£Ø1©2m£¬0£©£¬O”ä£Ø©![]() m£¬
m£¬![]() m£©£¬
m£©£¬

ÉčÖ±ĻßBB”äµÄ½āĪöŹ½ĪŖy=![]() x+b£¬°ŃR£Ø1©2m£¬0£©“śČė£¬µĆµ½b=
x+b£¬°ŃR£Ø1©2m£¬0£©“śČė£¬µĆµ½b=![]() £Ø2m©1£©£¬
£Ø2m©1£©£¬
”ąÖ±ĻßB”äC”äµÄ½āĪöŹ½ĪŖy=![]() x+
x+![]() £Ø2m©1£©£¬
£Ø2m©1£©£¬
”ąT£Ø©1£¬2![]() m©2
m©2![]() £©£¬
£©£¬
”ąO”äR2=£Ø![]() m©1£©2+£Ø
m©1£©2+£Ø![]() m£©2£¬O”äT2=£Ø1©
m£©2£¬O”äT2=£Ø1©![]() m£©2+£Ø2
m£©2+£Ø2![]() ©
©![]() m£©2£¬RT2=£Ø2©2m£©2+£Ø2
m£©2£¬RT2=£Ø2©2m£©2+£Ø2![]()
![]() ©2
©2![]() m£©2£¬
m£©2£¬
¢Łµ±O”äT=RTŹ±£¬£Ø1©![]() m£©2+£Ø2
m£©2+£Ø2![]() ©
©![]() m£©2=£Ø2©2m£©2+£Ø2
m£©2=£Ø2©2m£©2+£Ø2![]() ©2
©2![]() m£©2£¬
m£©2£¬
ÕūĄķµĆ£ŗ7m2©11m+3=0£¬
½āµĆm=![]() £¬
£¬
”ąR£Ø![]() £¬0£©»ņ£Ø
£¬0£©»ņ£Ø![]() £¬0£©£®
£¬0£©£®
¢Śµ±O”äT=O”äRŹ±£¬£Ø![]() m©1£©2+£Ø
m©1£©2+£Ø![]() m£©2=£Ø1©
m£©2=£Ø1©![]() m£©2+£Ø2
m£©2+£Ø2![]() ©
©![]() m£©2£¬
m£©2£¬
ÕūĄķµĆ£ŗ2m2©5m+6=0£¬
”÷£¼0ĪŽ½ā£®
¢Ūµ±RT=RO”䏱£¬£Ø![]() m©1£©2+£Ø
m©1£©2+£Ø![]() m£©2=£Ø2©2m£©2+£Ø2
m£©2=£Ø2©2m£©2+£Ø2![]() ©2
©2![]() m£©2£¬
m£©2£¬
ÕūĄķµĆ15m2©31m+15=0
½āµĆm=![]() £¬
£¬
”ąR£Ø![]() £¬0£©»ņ£Ø
£¬0£©»ņ£Ø![]() £¬0£©£®
£¬0£©£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖµćA£¬B£¬CŌŚ°ė¾¶ĪŖ4µÄ”ŃOÉĻ£¬¹żµćC×÷”ŃOµÄĒŠĻß½»OAµÄŃÓ³¤ĻßÓŚµćD£®
£Ø¢ń£©Čō”ĻABC=29”ć£¬Ēó”ĻDµÄ“󊔣»
£Ø¢ņ£©Čō”ĻD=30”ć£¬”ĻBAO=15”ć£¬×÷CE”ĶABÓŚµćE£¬Ēó£ŗ
¢ŁBEµÄ³¤£»
¢ŚĖıߊĪABCDµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼![]() ”¢Ķ¼
”¢Ķ¼![]() ”¢Ķ¼
”¢Ķ¼![]() £¬ŌŚ¾ŲŠĪ
£¬ŌŚ¾ŲŠĪ![]() ÖŠ£¬
ÖŠ£¬![]() ŹĒ
ŹĒ![]() ±ßÉĻµÄŅ»µć£¬ŅŌ
±ßÉĻµÄŅ»µć£¬ŅŌ![]() ĪŖ±ß×÷Ę½ŠŠĖıߊĪ
ĪŖ±ß×÷Ę½ŠŠĖıߊĪ![]() £¬Ź¹µć
£¬Ź¹µć![]() ŌŚ
ŌŚ![]() µÄ¶Ō±ß
µÄ¶Ō±ß![]() ÉĻ£¬
ÉĻ£¬
![]() ČēĶ¼
ČēĶ¼![]() £¬ŹŌĖµĆ÷£ŗĘ½ŠŠĖıߊĪ
£¬ŹŌĖµĆ÷£ŗĘ½ŠŠĖıߊĪ![]() µÄĆ껿Óė¾ŲŠĪ
µÄĆ껿Óė¾ŲŠĪ![]() µÄĆ껿ĻąµČ£»
µÄĆ껿ĻąµČ£»
![]() ČēĶ¼
ČēĶ¼![]() £¬ČōĘ½ŠŠĖıߊĪ
£¬ČōĘ½ŠŠĖıߊĪ![]() ŹĒ¾ŲŠĪ£¬
ŹĒ¾ŲŠĪ£¬![]() Óė
Óė![]() ½»ÓŚµć
½»ÓŚµć![]() £¬ŹŌĖµĆ÷£ŗ
£¬ŹŌĖµĆ÷£ŗ![]() ”¢
Ӣ![]() Ӣ
Ӣ![]() Ӣ
”¢![]() ĖĵćŌŚĶ¬Ņ»øöŌ²ÉĻ£»
ĖĵćŌŚĶ¬Ņ»øöŌ²ÉĻ£»
![]() ČēĶ¼
ČēĶ¼![]() £¬Čō
£¬Čō![]() £¬Ę½ŠŠĖıߊĪ
£¬Ę½ŠŠĖıߊĪ![]() ŹĒÕż·½ŠĪ£¬ĒŅ
ŹĒÕż·½ŠĪ£¬ĒŅ![]() ŹĒ
ŹĒ![]() µÄÖŠµć£¬
µÄÖŠµć£¬![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬ÅŠ¶ĻŅŌ
£¬ÅŠ¶ĻŅŌ![]() ĪŖÖ±¾¶µÄŌ²ÓėÖ±Ļß
ĪŖÖ±¾¶µÄŌ²ÓėÖ±Ļß![]() µÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®
µÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy=ax+b£Øa”Ł0£©ÓėyÖį½»ÓėµćC£¬ÓėĖ«ĒśĻßy=![]() £Øm”Ł0£©½»ÓŚA”¢BĮ½µć£¬AD”ĶyÖįÓŚµćD£¬Į¬½ÓBD£¬ŅŃÖŖOC=AD=2£¬cos”ĻACD=
£Øm”Ł0£©½»ÓŚA”¢BĮ½µć£¬AD”ĶyÖįÓŚµćD£¬Į¬½ÓBD£¬ŅŃÖŖOC=AD=2£¬cos”ĻACD=![]() £®
£®
£Ø1£©ĒóÖ±ĻßABŗĶĖ«ĒśĻߵĽāĪöŹ½£®
£Ø2£©Ēó”÷ABDµÄĆ껿£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
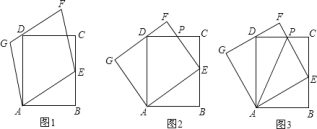
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÖŠ£¬”ĻABC=45”ć£¬¹żC×÷AB±ßÉĻµÄøßCD£¬HĪŖBC±ßÉĻµÄÖŠµć£¬Į¬½ÓDH£¬CDÉĻÓŠŅ»µćF£¬ĒŅAD=DF£¬Į¬½ÓBF²¢ŃÓ³¤½»ACÓŚE£¬½»DHÓŚG£®
£Ø1£©ČōAC=5£¬DH=2£¬ĒóDFµÄ³¤£®
£Ø2£©ČōAB=CB£¬ĒóÖ¤£ŗBG=![]() AE£®
AE£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ ”°ÉĶÖŠ»ŖŹ«“Ź£¬Ń°ĪĻƻłŅņ£¬Ę·Éś»ī֮ƥ”±£¬Ä³Š£¾Ł°ģĮĖŹ×½ģ”°ÖŠ¹śŹ«“Ź“ó»į”±£¬¾Ń”°ĪŗóÓŠ50Ćūѧɜ²Ī¼Ó¾öČü£¬Õā50ĆūѧɜĶ¬Ź±Ä¬Š“50Ź×¹ÅŹ«“Ź£¬ČōĆæÕżČ·Ä¬Š“³öŅ»Ź×¹ÅŹ«“ŹµĆ2·Ö£¬øł¾Ż²āŹŌ³É¼Ø»ęÖĘ³ö²æ·ÖʵŹż·Ö²¼±ķŗĶ²æ·ÖʵŹż·Ö²¼Ö±·½Ķ¼ČēĶ¼±ķ£ŗ
Ēė½įŗĻĶ¼±ķĶź³ÉĻĀĮŠø÷Ģā£ŗ
£Ø1£©¢Ł±ķÖŠaµÄÖµĪŖ £¬ÖŠĪ»ŹżŌŚµŚ ×飻
¢ŚĘµŹż·Ö²¼Ö±·½Ķ¼²¹³äĶźÕū£»
£Ø2£©Čō²āŹŌ³É¼Ø²»µĶÓŚ80·ÖĪŖÓÅŠć£¬Ōņ±¾“Ī²āŹŌµÄÓÅŠćĀŹŹĒ¶ąÉŁ£æ
£Ø3£©µŚ5×é10ĆūĶ¬Ń§ÖŠ£¬ÓŠ4ĆūÄŠĶ¬Ń§£¬ĻÖ½«Õā10ĆūĶ¬Ń§Ę½¾ł·Ö³ÉĮ½×é½ųŠŠ¶Ōæ¹Į·Ļ°£¬ĒŅ4ĆūÄŠĶ¬Ń§Ćæ×é·ÖĮ½ČĖ£¬ĒóŠ”Ć÷ÓėŠ”ĒæĮ½ĆūÄŠĶ¬Ń§ÄÜ·ÖŌŚĶ¬Ņ»×éµÄøÅĀŹ£®
×鱚 | ³É¼Øx·Ö | ʵŹż£ØČĖŹż£© |
µŚ1×é | 50”Üx£¼60 | 6 |
µŚ2×é | 60”Üx£¼70 | 8 |
µŚ3×é | 70”Üx£¼80 | 14 |
µŚ4×é | 80”Üx£¼90 | a |
µŚ5×é | 90”Üx£¼100 | 10 |

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±Ļßy£½£x£«1ÓėÅ×ĪļĻßy£½ax2£«bx£«c(a”Ł0)Ļą½»ÓŚµćA(1£¬0)ŗĶµćD(£4£¬5)£¬²¢ÓėyÖį½»ÓŚµćC£¬Å×ĪļĻߵĶŌ³ĘÖįĪŖÖ±Ļßx£½£1£¬ĒŅÅ×ĪļĻßÓėxÖį½»ÓŚĮķŅ»µćB.
(1)ĒóøĆÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
(2)ČōµćEŹĒÖ±ĻßĻĀ·½Å×ĪļĻßÉĻµÄŅ»øö¶Æµć£¬Ēó³ö”÷ACEĆ껿µÄ×ī“óÖµ£»
(3)ČēĶ¼2£¬ČōµćMŹĒÖ±Ļßx£½£1µÄŅ»µć£¬µćNŌŚÅ×ĪļĻßÉĻ£¬ŅŌµćA£¬D£¬M£¬NĪŖ¶„µćµÄĖıߊĪÄÜ·ń³ÉĪŖĘ½ŠŠĖıߊĪ£æČōÄÜ£¬ĒėÖ±½ÓŠ“³öµćMµÄ×ų±ź£»Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĶę¾ßµźÓĆ2000ŌŖ¹ŗ½ųŅ»ÅśĶę¾ß£¬Ćꏊŗ󣬹©²»Ó¦Ēó£¬ÓŚŹĒµźÖ÷ÓÖ¹ŗ½ųĶ¬ŃłµÄĶę¾ß£¬Ėł¹ŗµÄŹżĮæŹĒµŚŅ»ÅśŹżĮæµÄ3±¶£¬µ«Ć漞½ų¼Ū¹óĮĖ4ŌŖ£¬½į¹ū¹ŗ½ųµŚ¶žÅśĶę¾ß¹²ÓĆĮĖ6300ŌŖ.ČōĮ½ÅśĶę¾ßµÄŹŪ¼Ū¶¼ŹĒĆ漞120ŌŖ£¬ĒŅĮ½ÅśĶę¾ßČ«²æŹŪĶź£®
£Ø1£©µŚŅ»“Ī¹ŗ½ųĮĖ¶ąÉŁ¼žĶę¾ß£æ
£Ø2£©ĒóøĆĶę¾ßµźĻśŹŪÕāĮ½ÅśĶę¾ß¹²ÓÆĄū¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬Å×ĪļĻßy=ax2+bx+cÓė×ų±źÖį·Ö±š½»ÓŚµćA£Ø0£¬6£©£¬B£Ø6£¬0£©£¬C£Ø©2£¬0£©£¬µćPŹĒĻ߶ĪABÉĻ·½Å×ĪļĻßÉĻµÄŅ»øö¶Æµć£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©µ±µćPŌĖ¶Æµ½Ź²Ć“Ī»ÖĆŹ±£¬”÷PABµÄĆ껿ӊ×ī“óÖµ£æ
£Ø3£©¹żµćP×÷xÖįµÄ“¹Ļߣ¬½»Ļ߶ĪABÓŚµćD£¬ŌŁ¹żµćP×öPE”ĪxÖį½»Å×ĪļĻßÓŚµćE£¬Į¬½įDE£¬ĒėĪŹŹĒ·ń“ęŌŚµćPŹ¹”÷PDEĪŖµČŃüÖ±½ĒČż½ĒŠĪ£æČō“ęŌŚ£¬Ēó³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com