
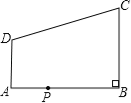
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=![]() ,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )

A. 1个
B. 2个
C. 3个
D. 4个
【答案】C
【解析】试题分析:由于∠PAD=∠PBC=90°,故要使△PAD与△PBC相似,分两种情况讨论:①△APD∽△BPC,②△APD∽△BCP,这两种情况都可以根据相似三角形对应边的比相等求出AP的长,即可得到P点的个数.
解:∵AB⊥BC,
∴∠B=90°.
∵AD∥BC,
∴∠A=180°﹣∠B=90°,
∴∠PAD=∠PBC=90°.AB=8,AD=3,BC=4,
设AP的长为x,则BP长为8﹣x.
若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:
①若△APD∽△BPC,则AP:BP=AD:BC,即x:(8﹣x)=3:4,解得x=![]() ;
;
②若△APD∽△BCP,则AP:BC=AD:BP,即x:4=3:(8﹣x),解得x=2或x=6.
∴满足条件的点P的个数是3个,
故选:C.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】点 P(﹣2,﹣3)向右平移 2 个单位,再向上平移 4 个单位,则所得到的点的坐标为( )
A. (﹣2,0) B. (0,﹣2) C. (1,0) D. (0,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
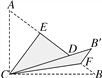
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4.将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016·毕节中考)如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
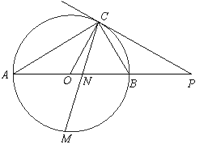
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线![]() ,点
,点![]() 、
、![]() 分别在直线
分别在直线![]() ,
,![]() 上,点
上,点![]() 为平面内一点.
为平面内一点.
(![]() )如图,
)如图,![]() ,
,![]() ,
,![]() 的数量关系是__________.
的数量关系是__________.

(![]() )利用(
)利用(![]() )的结论解决问题:如图,已知
)的结论解决问题:如图,已知![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,求
,求![]() 得度数.
得度数.

(![]() )如图,点
)如图,点![]() 为
为![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,直接写出
,直接写出![]() ,
,![]() ,
,![]() 之间的数量关系.(用含
之间的数量关系.(用含![]() 的式子表示)
的式子表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com