练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知a+b＝3，则a2﹣b2+6b的值是（　　）

    A.2B.3C.9D.6

    【答案】C

    【解析】

    将所求的代数式化成含有(a+b)的式子，将(a+b)作为一个整体代入求值即可．

    a2﹣b2+6b

    ＝（a+b）(a﹣b)+6b

    ＝3(a﹣b）+6b

    ＝3a+3b

    ＝3(a+b)

    ＝9．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，以O（0，0）、A（1，-1）、B（2，0）为顶点，构造平行四边形，下列各点中不能作为平行四边形第四个顶点坐标的是（　　　）

    A. （3，-1） B. （-1，-1） C. （1，1） D. （-2，-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：求59319的立方根．华罗庚脱口而出：39．众人感觉十分惊奇，请华罗庚给大家解读了其中的奥秘.

    你知道怎样迅速准确的计算出结果吗？请你按下面的问题试一试：

    ①，，又，

    ，

    能确定59319的立方根是个两位数．

    ②59319的个位数是9，又，

    能确定59319的立方根的个位数是9．

    ③如果划去59319后面的三位319得到数59，

    而，则，可得，

    由此能确定59319的立方根的十位数是3

    因此59319的立方根是39.

    （1）现在换一个数110592，按这种方法求立方根，请完成下列填空.

    ①它的立方根是 位数．

    ②它的立方根的个位数是 ．

    ③它的立方根的十位数是 ．

    ④110592的立方根是 ．

    （2）请直接填写结果：

    ① ；

    ② ；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平行四边形ABCD中，E是AD上一点，AE=AB，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG．

    （1）如图①，当EF与AB相交时，若∠EAB=60°，求证：EG=AG+BG；

    （2）如图②，当EF与CD相交时，且∠EAB=90°，请你写出线段EG、AG、BG之间的数量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，A（-1，5），B（-1，0），C（-4，3）．

    （1）求ΔABC的面积；

    （2）在图中画出ΔABC向右平移3个单位，再向下平移2个单位的图形△A1B1C1；

    （3）写出点A1，B1，C1的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】命题：“两个角的和等于平角时，这两个角互为邻补角”是_____命题（填“真”或“假”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校开展了以“人生观、价值观”为主题的班队活动．活动结束后，初三（2）班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调査（要求每位同学只选自己最认可的一项观点），并制成了如图所示的扇形统计图．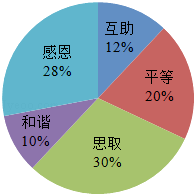
    （1）该班学生选择“和谐”观点的有人，在扇形统计图中，“和谐”观点所在扇形区域的圆心角是 ．
    （2）如果该校有1500名初三学生．利用样本估计选择“感恩”观点的初三学生约有人．
    （3）如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查．求恰好选到“和谐”和“感恩”观点的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校120名学生某一周用于阅读课外书籍的时间的频率分布直方图如图所示．其中阅读时间是8~10小时的频数和频率分别是( )

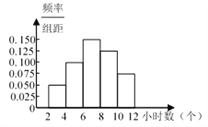
    A. 15和0.125 B. 15和0.25 C. 30和0.125 D. 30和0.25

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】放风筝是大家喜爱的一种运动．星期天的上午小明在大洲广场上放风筝．如图他在A处时不小心让风筝挂在了一棵树的树梢上，风筝固定在了D处．此时风筝线AD与水平线的夹角为30°． 为了便于观察．小明迅速向前边移动边收线到达了离A处7米的B处，此时风筝线BD与水平线的夹角为45°．已知点A、B、C在冋一条直线上，∠ACD=90°．请你求出小明此吋所收回的风筝线的长度是多少米？（本题中风筝线均视为线段， ≈1.414， ≈1.732．最后结果精确到1米）

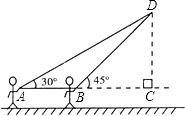
    查看答案和解析>>

    同步练习册答案