
【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.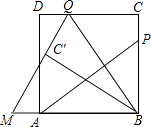
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.
【答案】
(1)解:AP=BQ.
理由:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°,
∴∠ABQ+∠CBQ=90°.
∵BQ⊥AP,∴∠PAB+∠QBA=90°,∴∠PAB=∠CBQ.
在△PBA和△QCB中,
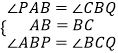 ,
,
∴△PBA≌△QCB,
∴AP=BQ
(2)解:过点Q作QH⊥AB于H,如图. 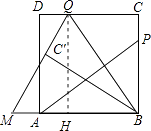
∵四边形ABCD是正方形,
∴QH=BC=AB=3.
∵BP=2PC,
∴BP=2,PC=1,
∴BQ=AP= ![]() =
= ![]() =
= ![]() ,
,
∴BH= ![]() =
= ![]() =2.
=2.
∵四边形ABCD是正方形,
∴DC∥AB,
∴∠CQB=∠QBA.
由折叠可得∠C′QB=∠CQB,
∴∠QBA=∠C′QB,
∴MQ=MB.
设QM=x,则有MB=x,MH=x﹣2.
在Rt△MHQ中,
根据勾股定理可得x2=(x﹣2)2+32,
解得x= ![]() .
.
∴QM的长为 ![]()
(3)解:过点Q作QH⊥AB于H,如图. 
∵四边形ABCD是正方形,BP=m,PC=n,
∴QH=BC=AB=m+n.
∴BQ2=AP2=AB2+PB2,
∴BH2=BQ2﹣QH2=AB2+PB2﹣AB2=PB2,
∴BH=PB=m.
设QM=x,则有MB=QM=x,MH=x﹣m.
在Rt△MHQ中,
根据勾股定理可得x2=(x﹣m)2+(m+n)2,
解得x=m+n+ ![]() ,
,
∴AM=MB﹣AB=m+n+ ![]() ﹣m﹣n=
﹣m﹣n= ![]() .
.
∴AM的长为 ![]() .
.
【解析】(1)由正方形的性质得出AB=BC,∠ABC=∠C=90°,由同角的余角相等得出∠PAB=∠CBQ.进而利用ASA得出△PBA≌△QCB,,由全等三角形对应边相等得出结论;
(2)过点Q作QH⊥AB于H,由正方形的性质得出QH=BC=AB=3.结合已知 条件得出BP=2,PC=1,进而根据勾股定理求出BH的长,再由折叠的性质得到∠C′QB=∠CQB,从而得到MQ=MB,设QM=x,则有MB=x,MH=x﹣2,在Rt△MHQ中,根据勾股定理得出方程,解方程得到x的值,即可;
(3)过点Q作QH⊥AB于H,由正方形的性质得出QH=BC=AB=m+n,结合已知 条件得出BP=m,PC=n,进而根据勾股定理求出BH的长,再由折叠的性质得到∠C′QB=∠CQB,从而得到MQ=MB,设QM=x,则有MB=x,MH=x﹣m,在Rt△MHQ中,根据勾股定理得出方程,解方程得到x的值,即可;
【考点精析】利用勾股定理的概念和正方形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,以A(0, ![]() )为圆心的圆与x轴相切于坐标原点O,与y轴相交于点B,弦BD的延长线交x轴的负半轴于点E,且∠BEO=60°,AD的延长线交x轴于点C.
)为圆心的圆与x轴相切于坐标原点O,与y轴相交于点B,弦BD的延长线交x轴的负半轴于点E,且∠BEO=60°,AD的延长线交x轴于点C.
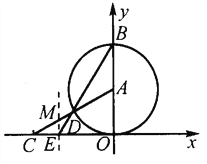
(1)分别求点E、C的坐标;
(2)求经过A、C两点,且以过E而平行于y轴的直线为对称轴的抛物线的函数解析式;
(3)设抛物线的对称轴与AC的交点为M,试判断以M点为圆心,ME为半径的圆与⊙A的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式由左到右的变形中,属于因式分解的是( )
A. a(m+n)= am+an B. a2﹣b2﹣c2 =(a﹣b)(a+b)﹣c2
C. 10x2﹣5x = 5x(2x﹣1) D. x2﹣16+6x =(x+4)(x﹣4)+ 6x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).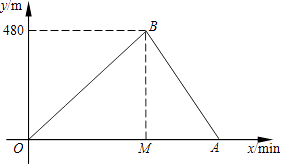
(1)A点所表示的实际意义是; ![]() =;
=;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中任意一点p(x,y)经平移后对应点为p1(x+5,y+3),将△ABC作同样的平移得到△A1B1C1.
(1)画出△A1B1C1;
(2)求A1,B1,C1的坐标;
(3)写出平移的过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果收入100元记作+100元.那么﹣80元表示( )
A.支出20元
B.收入20元
C.支出80元
D.收入80元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com