
【题目】如图,△ABE中,点A、B是反比例函数y=![]() (k≠0)图象上的两点,点E在x轴上,延长线段AB交y轴于点C,点B恰为线段AC中点,过点A作AD⊥x轴于点D.若S△ABE=
(k≠0)图象上的两点,点E在x轴上,延长线段AB交y轴于点C,点B恰为线段AC中点,过点A作AD⊥x轴于点D.若S△ABE=![]() ,DE=2OE,则k的值为( )
,DE=2OE,则k的值为( )
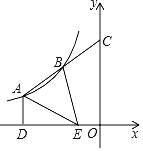
A.6B.﹣6C.9D.﹣9
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
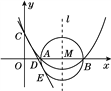
【题目】如图,已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的表达式及A,B两点的坐标.
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值;若不存在,请说明理由;
(3)在以AB为直径的⊙M中,CE与⊙M相切于点E,CE交x轴于点D,求直线CE的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】C,D两城蔬菜紧缺,A,B两城决定支援,A城有蔬菜20吨,B城有蔬菜40吨,C城需要蔬菜16吨,D城需要蔬菜44吨,已知A到C,D的运输费用分别为200元/吨,220元/吨,B到C,D的运输费用分别为300元/吨,340元/吨,规定A向C城运的吨数不小于B向C城运的吨数,设A城向C城运x吨,请回答下列问题:
(1)根据题意条件,填写下列表格:

(2)设总费用为y(元),求出y(元)与x(吨)的函数关系式,并写出x的取值范围;
(3)怎样调运货物能使总费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2016年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2018年底三年累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2018年底共建设了多少万平方米廉租房.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②a﹣b+c<0;③4a+b+c=0;④抛物线的顶点坐标为(2,b);⑤当x<1时,y随x增大而增大.其中结论正确的是( )
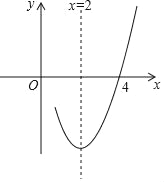
A. ①②③ B. ①④⑤ C. ①③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,E为线段BC上一点,AE交CD于G,且GC=GE,EF⊥BC交AB于点F.
(1)求证:AE2=AFAB;
(2)连FG,若BE=2CE,求tan∠AFG;
(3)如图2,当tanB= 时,CE=FE(请直接写出结果,不需要解答过程).
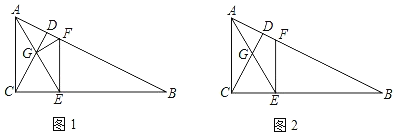
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】恒昌路是一条东西走向的马路,有市场、医院、车站、学校四家公共场所。已知市场在医院东200米,车站在市场东150米,医院在学校东450米。若将马路近似的看成一条直线,以医院为原点,向东方向为正方向,用1个单位长度表示100米,
(1)在数轴上表示出四家公共场所的位置;
![]()
(2)列式计算学校与车站之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明.如图,已知AB∥CD,∠B=∠C,
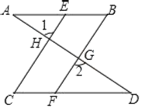
求证:∠1=∠2.
证明:∵AB∥CD(已知)
∴∠B= ( ).
∵∠B=∠C(已知)
∴∠BFD=∠C(等量代换)
∴EC∥ ( )
∴∠2= (两直线平行,同位角相等)
∵∠1= ( )
∴∠1=∠2(等量代换).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com