
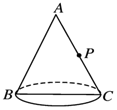
 已知如图,圆锥的母线长6cm,底面半径是3cm,在B处有一只蚂蚁,在AC中点P处有一颗米粒,蚂蚁从B爬到P处的最短距离是( )
已知如图,圆锥的母线长6cm,底面半径是3cm,在B处有一只蚂蚁,在AC中点P处有一颗米粒,蚂蚁从B爬到P处的最短距离是( )| A. | 3$\sqrt{3}$cm | B. | 3$\sqrt{5}$cm | C. | 9cm | D. | 6cm |
分析 将圆锥的侧面展开,根据“两点之间线段最短”可得出蚂蚁爬行的最短路线及最短的路程.
解答 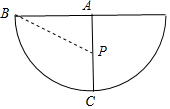 解:∵圆锥的侧面展开图是一个扇形,设该扇形的圆心角为n,
解:∵圆锥的侧面展开图是一个扇形,设该扇形的圆心角为n,
则:$\frac{nπr}{180}$=$\frac{1}{2}$×2×3π,其中r=3,
∴n=180°,如图所示:
由题意可知,AB⊥AC,且点P为AC的中点,
在Rt△ABP中,AB=6,AP=3,
∴BP=$\sqrt{A{B}^{2}+A{P}^{2}}$=3$\sqrt{5}$cm,
故蚂蚁沿线段Bp爬行,路程最短,最短的路程是3$\sqrt{5}$cm.
点评 本题考查了平面展开-最短路径问题,用到的知识点:圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
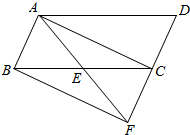 如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.
如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
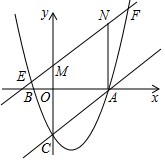 已知抛物线y=x2-2x-3,与x轴交于A、B两点,与y轴交于C点,EF∥AC交y轴于M,AN∥y轴交EF于N点,求$\frac{EM}{FN}$的值.
已知抛物线y=x2-2x-3,与x轴交于A、B两点,与y轴交于C点,EF∥AC交y轴于M,AN∥y轴交EF于N点,求$\frac{EM}{FN}$的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com