
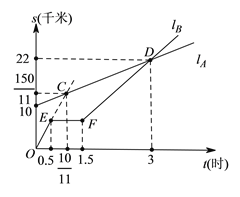
【题目】如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距______千米.
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
(3)B出发后______小时与A相遇.
(4)若B的自行车不发生故障,保持出发时的速度前进,______小时与A相遇,相遇点离B的出发点______千米.在图中表示出这个相遇点C.
(5)求出A行走的路程S与时间t的函数关系式。

【答案】(1)10;(2)1;(3)3;(4)![]() ,
, ![]() ;(5)S=4t+10.
;(5)S=4t+10.
【解析】试题分析:
(1)由图可知,B出发时与A相距10km;
(2)由图可知,B修自行车所用时间为:1.5-0.5=1(小时);
(3)由图象可知,B在出发后3小时的时候与A相遇;
(4)分别求出![]() 的函数关系式和
的函数关系式和![]() 在修车前的函数关系式,由两个解析式组成方程组,解方程组,即可求得所求答案.
在修车前的函数关系式,由两个解析式组成方程组,解方程组,即可求得所求答案.
试题解析:
(1)由图和题意可得:B出发时与A相距10千米.
故答案为:10;
(2)由图和题意可得:修理自行车的时间为:1.5-05=1(小时).
故答案为:1;
(3)由图象可得:B出发3小时时和A相遇,
故答案为:3;
(4)设lA的解析式为:S1=at+b,
∵lA过点(0,10)和(3,22),
∴![]() ,
,
解得: ![]() ,
,
∴S1=4t+10,
设B修车前的关系式为:S2=kt,
∵修车前lB过(0.5,7.5)点.
∴7.5=0.5k,解得:k=15,
∴S2=15t,
由![]() ,解得:
,解得:  ,
,
即若B的自行车不发生故障,保持出发时的速度前进,则![]() 小时时相遇,此时B走的路程是
小时时相遇,此时B走的路程是![]() 千米.在图中用点C表示相遇点如下图所示:
千米.在图中用点C表示相遇点如下图所示:
(5)由(4)得:A行走的路程S与时间t的函数关系式为:S=4t+10.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y= ![]() (x>0)的图象经过顶点B,则反比例函数的表达式为( )
(x>0)的图象经过顶点B,则反比例函数的表达式为( ) 
A.y= ![]()
B.y= ![]()
C.y= ![]()
D.y= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)(﹣ab)3(5a2b﹣4ab2);
(2)(2x﹣1)(4x2+2x+1)
(3)求5x(2x+1)﹣(2x+3)(5x﹣1)的值,其中x=12.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法: ①c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④am2+bm+a>0(m≠﹣1).
其中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠DOE=![]() ∠BOD,∠COE=72°,则∠EOB=( )
∠BOD,∠COE=72°,则∠EOB=( )
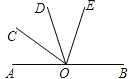
A. 36° B. 72°
C. 108° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
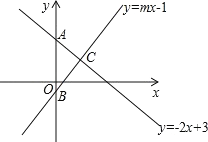
【题目】如图,直线y1=-2x+3和直线y2=mx-3分别交y轴于点A、B ,两直线交于点C(1,n).
(1)求 m、n 的值;
(2)求△ABC的面积;
(3)请根据图象直接写出:当 y1<y2时,自变量 x 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形ABCD、CEFG均为正方形. 
(1)求证:BE=DG.
(2)如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.是否仍存在结论BE=DG,若不存在,请说明理由;若存在,给出证明. 
(3)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为降低空气污染,公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年均载客量如表:
A型 | B型 | |
价格(万元/辆) | a | b |
年均载客量(万人/年/辆) | 60 | 100 |
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元
(1)求购买每辆A型公交车和每辆B型公交车分别多少万元?
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车年均载客总和不少于680万人次,有哪几种购车方案?请你设计一个方案,使得购车总费用最少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com