
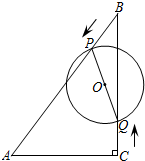
 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0≤t≤2),连接PQ,以PQ为直径作⊙O.
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0≤t≤2),连接PQ,以PQ为直径作⊙O.分析 (1)过点P作PM⊥BC于点M,根据△BPM∽△BAC,可得PM=3t,BM=4t,然后得到S△BPQ=$\frac{1}{2}$BQ•PM=12t-6t2,代入当t=0.5时,求得S△BPQ=4.5即可;
(2)表示出有关t的二次函数求得最小值是t的取值即可;
(3)分当⊙O与BC相切时、当⊙O与AB相切时当⊙O与AC相切时三种情况分类讨论即可确定正确的选项.
解答 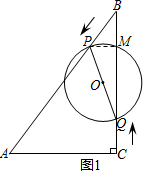 解:(1)如图1,过点P作PM⊥BC于点M,
解:(1)如图1,过点P作PM⊥BC于点M,
△BPM∽△BAC,可得PM=3t,BM=4t,S△BPQ=$\frac{1}{2}$BQ•PM=12t-6t2,
∴当t=0.5时,S△BPQ=4.5;
(2)MQ=|8-8t|,PQ2=PM2+MQ2=(8-8t)2+(3t)2=73t2-128t+64,
∴$y=\frac{π}{4}P{Q^2}=\frac{73π}{4}{t^2}-32πt+16π$,
当t=$\frac{64}{73}$时,y的值最小.
(3)当⊙O与BC相切时,PQ⊥BC,△BPQ∽△BAC,
∴$\frac{BP}{BA}=\frac{BQ}{BC}$,
∴$\frac{5t}{10}=\frac{8-4t}{8}$,
∴t1=1,
当⊙O与AB相切时,PQ⊥AB,△BPQ∽△BCA
∴$\frac{BP}{BC}=\frac{BQ}{BA}$,∴$\frac{5t}{8}=\frac{8-4t}{10}$,
∴t2=$\frac{32}{41}$,
当⊙O与AC相切时,
如图2,过点O作OH⊥AC于点H,交PM于点N,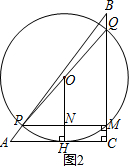
OH=ON+NH=$\frac{1}{2}$QM+MC=$\frac{1}{2}$(8t-8)+(8-4t)=4,
∴PQ=2OH=8,
∴73t2-128t+64=64
解得t3=0,t4=$\frac{128}{73}$,
综上所述,若⊙O与Rt△ABC的一条边相切,
t的值为1或$\frac{32}{41}$或0或$\frac{128}{73}$.
点评 本题考查了相似三角形的判定与性质及圆的综合知识;由三角形相似得出对应边成比例是解题的关键,此类题目为中考的热点考题之一,应加强训练.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
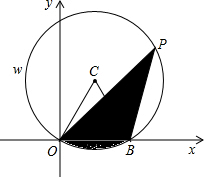 如图,在平面直角坐标系xOy中,⊙C经过点O,交x轴的正半轴于点B(2,0),P是$\widehat{OwB}$上的一个动点,且∠OPB=30°.设P点坐标为(m,n)
如图,在平面直角坐标系xOy中,⊙C经过点O,交x轴的正半轴于点B(2,0),P是$\widehat{OwB}$上的一个动点,且∠OPB=30°.设P点坐标为(m,n)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
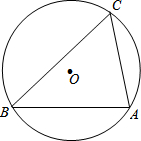 对于一个三角形,设其三个内角的度数分别为x°、y°和z°,若x、y、z满足x2+y2=z2,我们定义这个三角形为美好三角形.
对于一个三角形,设其三个内角的度数分别为x°、y°和z°,若x、y、z满足x2+y2=z2,我们定义这个三角形为美好三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
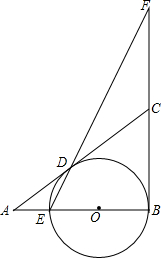 如图,在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连结ED,且延长交BC的延长线于点F.
如图,在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连结ED,且延长交BC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x}{2}$+$\frac{y}{4}$=-1 | B. | xy+z=5 | C. | 2x2+3y-5=0 | D. | 2x+$\frac{1}{y}$=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
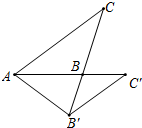 如图,△ABC中,∠ABC>90°,tan∠BAC=$\frac{3}{4}$,BC=4,将三角形绕着点A旋转,点C落在直线AB上的点C′处,点B落在点B′处.若C、B、B′恰好在一直线上,则AB的长为$\frac{6\sqrt{10}}{5}$.
如图,△ABC中,∠ABC>90°,tan∠BAC=$\frac{3}{4}$,BC=4,将三角形绕着点A旋转,点C落在直线AB上的点C′处,点B落在点B′处.若C、B、B′恰好在一直线上,则AB的长为$\frac{6\sqrt{10}}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com