
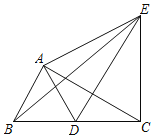
【题目】如图,在等腰△ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB延长线于点E,垂足为点F.
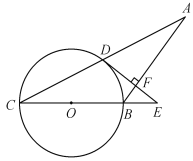
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径R=5,且tanC =![]() ,求EF的长.
,求EF的长.
【答案】(1)相切;(2)![]()
【解析】
(1)连接圆心和切点,利用平行,OF⊥CB可证得∠ODF=90°;
(2)过D作DH⊥BC于H,设BD=k,CD=2k,求得BD=2![]() ,CD=4
,CD=4![]() ,根据三角形的面积公式得到DH=
,根据三角形的面积公式得到DH=![]() =4,由勾股定理得到OH=
=4,由勾股定理得到OH=![]() =3,根据三角形相似得到OD2=OHOE,求得OE=
=3,根据三角形相似得到OD2=OHOE,求得OE=![]() ,得到BE=
,得到BE=![]() ,根据相似三角形的性质得到BF=2,根据勾股定理即可得到结论.
,根据相似三角形的性质得到BF=2,根据勾股定理即可得到结论.
(1)证明:如图,连接OD,BD,

∵BC是⊙O的直径,
∴∠CDB=90°,
∴BD⊥AC.
∵AB=BC,
∴AD=DC.
∵OC=OB,
∴OD∥AB,
∵DE⊥AB,
∴DE⊥OD.
∴直线DE是⊙O的切线.
(2)过D作DH⊥BC于H,
∵⊙O的半径R=5,tanC=![]() ,
,
∴BC=10,
设BD=k,CD=2k,
∴BC=![]() k=10,
k=10,
∴k=2![]() ,
,
∴BD=2![]() ,CD=4
,CD=4![]() ,
,
∴DH=![]() =4,
=4,
∴OH=![]() =3,
=3,
∵DE⊥OD,DH⊥OE,
∴OD2=OHOE,
∴OE=![]() ,
,
∴BE=![]() ,
,
∵DE⊥AB,
∴BF∥OD,
∴△BFE∽△ODE,
∴![]() ,即
,即![]() ,
,
∴BF=2,
∴EF=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )

A. ![]() B. 2
B. 2![]() -
-![]() C. 2
C. 2![]() -
-![]() D. 4
D. 4![]() -
-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组由3名男生和1名女生组成,在一次合作学习后,开始进行成果展示.
(1)如果随机抽取1名同学单独展示,那么女生展示的概率为 ;
(2)如果随机抽取2名同学共同展示,求同为男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于C,D,交AB于E,AF为⊙O的直径,下列结论中正确的有:①∠ABP=∠AOP;②AP=BP;③弧BC=弧DF ;④∠APO=∠BPO;⑤AB⊥PD.
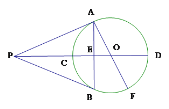
A. ①⑤ B. ②③⑤ C. ①④ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与A,C重合),延长BD至E.
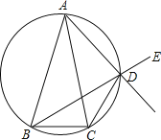
(1)求证:AD的延长线平分∠CDE;
(2)若∠BAC=30°,且△ABC底边BC边上高为1,求△ABC外接圆的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上.
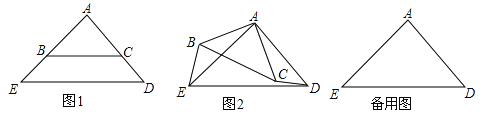
(1)请直接写出线段BE与线段CD的关系: ;
(2)如图2,将图1中的△ABC绕点A顺时针旋转角α(0<α<360°),
①(1)中的结论是否成立?若成立,请利用图2证明;若不成立,请说明理由;
②当AC=![]() ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两个全等的直角三角尺ABC和ADE如图摆放,∠CAB=∠DAE=90°,∠ACB=∠DEA=30°,使点D落在BC边上,连结EB,EC,则下列结论:①∠DAC=∠DCA;②ED为AC的垂直平分线;③EB平分∠AED;④△ACE为等边三角形.其中正确的是( )
A.①②③B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,E是CD延长线上的一点,BE与AD交于点F,DE=![]() CD.
CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车4S店销售某种型号的汽车,每辆进货价为15万元,该店经过一段时间的市场调研发现:当销售价为25万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出1辆.该4S店要想平均每周的销售利润为90万元,并且使成本尽可能的低,则每辆汽车的定价应为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com