
【题目】图1是一辆吊车的实物图,图2是其工作示意图,![]() 是可以伸缩的起重臂,其转动点
是可以伸缩的起重臂,其转动点![]() 离地面
离地面![]() 的高度
的高度![]() 为
为![]() .当起重臂
.当起重臂![]() 长度为
长度为![]() ,张角
,张角![]() 为118°.
为118°.
(1)求操作平台![]() 离地面的高度;
离地面的高度;
(2)当张角![]() 为120°,其它条件不变时,求操作平台
为120°,其它条件不变时,求操作平台![]() 升高的高度.
升高的高度.
(最后结果精确到0.1,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】(1)操作平台C离地面的高度为7.6m;(2)操作平台![]() 升高的高度为0.3m.
升高的高度为0.3m.
【解析】
(1)作CE⊥BD于E,AF⊥CE于F,如图2,易得四边形AHEF为矩形,则EF=AH=3.5m,∠HAF=90°,再计算出∠CAF=28°,则在Rt△ACF中利用正弦可计算出CF,然后计算CF+EF即可;
(2)作GQ⊥BD,垂足为Q,交AF于点P,求出GP的长,即可求出GQ的长,然后用GQ-CE即可得到答案.
(1)解:作CE⊥BD于E,AF⊥CE于F,如图,
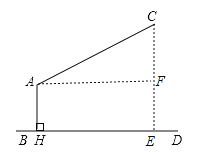
易得四边形AHEF为矩形,
∴EF=AH=3.4m,∠HAF=90°,
∴∠CAF=∠CAH-∠HAF=118°-90°=28°,
在Rt△ACF中,∵sin∠CAF=![]() ,
,
∴CF=9sin28°=9×0.47=4.23,
∴CE=CF+EF=4.23+3.4≈7.6(m),
答:操作平台C离地面的高度为7.6m.
(2)如图,作GQ⊥BD,垂足为Q,交AF于点P,易知PQ=3.4m,
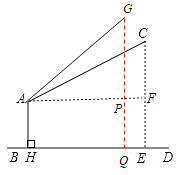
由(1)知,∠HAF=90°,AG=AC=9m,
∴∠GAF=∠GAH-∠HAF=120°-90°=30°,
在Rt△AGP中,∵sin∠GAP=![]() ,
,
∴GP=9sin30°=9×0.5=4.5,
∴GQ=GP+PQ=4.5+3.4=7.9m,
∴操作平台![]() 升高的高度为:GQ-CE=7.9-7.6=0.3m.
升高的高度为:GQ-CE=7.9-7.6=0.3m.


科目:初中数学 来源: 题型:
【题目】如图所示,菱形ABCD的边长是2厘米,∠BAD=120°,动点M以1厘米/秒的速度自A点出发向B移动,动点N以2厘米/移的速度自B点出发向D移动,两点中任一个到达线段端点移动便告结束.若点M、N同时出发运动了t秒,记△BMN的面积为S厘米2,下面图象中能表示S与t之间的函数关系的是( )
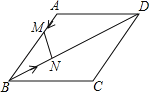
A.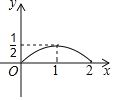 B.
B.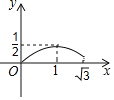
C.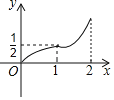 D.
D.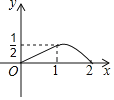
查看答案和解析>>
科目:初中数学 来源: 题型:
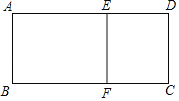
【题目】如图所示,用一根长度为18米的原材料制作一个矩形窗户边框(即矩形ABFE和矩形DCFE),原材料刚好全部用完,设窗户边框AB长度为x米,窗户总面积为S平方米(注:窗户边框粗细忽略不计).
(1)求S与x之间的函数关系式;
(2)若窗户边框AB的长度不少于2米,且边框AB的长度小于BC的长度,求此时窗户总面积S的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
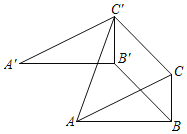
【题目】定义:有一组邻边相等的凸四边形叫做等邻边四边形.如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将△ABC沿∠ABC的平分线BB'的方向平移,得到A'B'C',连接AC',CC',若四边形ABCC'是等邻边四边形,则平移距离BB'的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
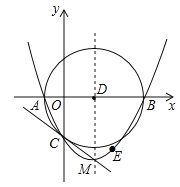
【题目】如图,抛物线y=![]() (x+2)(x﹣8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是( )
(x+2)(x﹣8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】表中所列![]() 、
、![]() 的7对值是二次函数
的7对值是二次函数![]() 图象上的点所对应的坐标,其中
图象上的点所对应的坐标,其中![]()
| … |
|
|
|
|
|
|
| … |
| … | 6 |
| 11 |
| 11 |
| 6 | … |
根据表中提供约信息,有以下4个判断:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 的值是
的值是![]() ;④
;④![]() ;其中判断正确的是( )
;其中判断正确的是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(2,y1),B(﹣3,y2),C(﹣5,y3)三个点都在反比例函数![]() 的图象上,比较y1,y2,y3的大小,则下列各式正确的是( )
的图象上,比较y1,y2,y3的大小,则下列各式正确的是( )
A.y1<y2<y3B.y2<y3<y1C.y1<y3<y2D.y3<y2<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
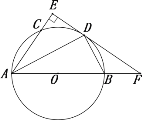
【题目】如图,AB是⊙O的直径,AD平分∠BAC交⊙O于D,过D作DE⊥AC交AC延长线于点E,交AB延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若DE=![]() ,tan∠BDF=
,tan∠BDF=![]() ,求DF的长.
,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com