
【题目】如图,□ ABCD中,E是AD边上一点,AD=4![]() ,CD=3,ED=
,CD=3,ED=![]() ,∠A=45.点P,Q分别是BC,CD边上的动点,且始终保持∠EPQ=45°.将
,∠A=45.点P,Q分别是BC,CD边上的动点,且始终保持∠EPQ=45°.将 ![]() CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,线段BP的长为________.
CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,线段BP的长为________.

【答案】![]() ,3,
,3,![]()
【解析】过点B作BF⊥AD于点F,连接BE,根据平行四边形的性质及已知条件,可证得△BEF是等腰直角三角形,求出BF、BE、的长,再利用三角形的外角性质结合已知,证明∠2=∠1,∠EBP=∠C,利用相似三角形的判定,可证得△BPE∽△CQP,再分三种情况讨论:①当CQ=QP时,则BP=PE,可证得四边形BPEF是矩形,可求出BP的长;②当CP=CQ时,则BP=BE=3;③当CP=PQ时,则BE=PE=3,再根据△BPE是等腰直角三角形,利用勾股定理,可求出BP的长,从而可得出答案.
如图,过点B作BF⊥AD于点F,连接BE
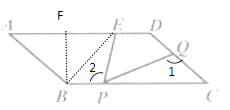
∵平行四边形ABCD
∴AD∥BC
∴∠BFE=∠FBP=90°
在Rt△ABF中,∠A=45°,AB=3
∴BF=AF=ABcos45°=3×![]() =
=![]()
∴EF=AD-AF-DE=4![]() -
-![]() -
-![]() =
=![]()
∴EF=BF
∴∠FBE=∠EBP=45°=∠C
∠2+∠EFQ=∠1+∠C
∵∠EFQ=∠C=45°
∴∠2=∠1
∴△BPE∽△CQP
将 △ CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,分三种情况:
①当CQ=QP时,则BP=PE
∴∠EBP=∠BEP=45°,则∠BPE=90°
∴四边形BPEF是矩形
∴BP=EF=![]()
②当CP=CQ时,则BP=BE=3
③当CP=PQ时,则BE=PE=3,∠BEP=90°
∴△BPE是等腰直角三角形
∴BP=![]() .
.
故答案为:![]() 、3、
、3、![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D…的规律绕在ABCD的边上,则细线另一端所在位置的点的坐标是( )

A. (0,-2) B. (-1,-1) C. (-1,0) D. (1,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC=______度;
(2)求∠EDF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )
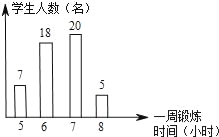
A. 平均数是6.5
B. 中位数是6.5
C. 众数是7
D. 平均每周锻炼超过6小时的人占总数的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE;⑤CF=BD.正确的有( )个.

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.

(1)∠1与∠2有什么关系,为什么?
(2)BE与DF有什么关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……,按这样的运动规律,经过第2018次运动后,动点P的坐标是( )

A. (2018,1)B. (2018,0)C. (2018,2)D. (2017,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
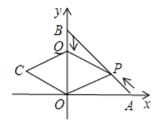
【题目】如图,A,B两点的坐标分别为(6,0),(0,6),点P从点A出发,沿AB方向以每秒![]() 个单位的速度向终点B运动;同时动点Q从点B出发沿BO方向以每秒1个单位的速度向终点Q运动,将△PQO沿BO翻折,点P的对应点为点C,若四边形QPOC为菱形,则点C的坐标为________.
个单位的速度向终点B运动;同时动点Q从点B出发沿BO方向以每秒1个单位的速度向终点Q运动,将△PQO沿BO翻折,点P的对应点为点C,若四边形QPOC为菱形,则点C的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
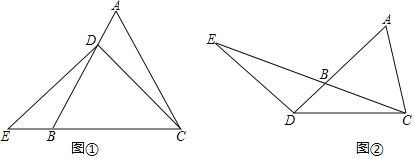
【题目】已知△ABC是等边三角形,点D是直线AB上一点,延长CB到点E,使BE=AD,连接DE,DC,
(1)若点D在线段AB上,且AB=6,AD=2(如图①),求证:DE=DC;并求出此时CD的长;
(2)若点D在线段AB的延长线上,(如图②),此时是否仍有DE=DC?请证明你的结论;
(3)在(2)的条件下,连接AE,若![]() ,求CD:AE的值.
,求CD:AE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com