
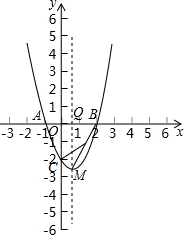
 已知二次函数的图象如图所示,抛物线与x轴、y轴分别交于点A(-1,0)、B(2,0)、C(0,-2).
已知二次函数的图象如图所示,抛物线与x轴、y轴分别交于点A(-1,0)、B(2,0)、C(0,-2).分析 (1)利用待定系数法求二次函数的解析式,并利用配方法求顶点M的坐标;
(2)如图1,先求直线BM的解析式为:y=$\frac{3}{2}$x-3,设N(h,-t),因为点N在线段MB上运动,所以把点N(h,-t)代入y=$\frac{3}{2}$x-3得:h=2-$\frac{2}{3}$t,其中$\frac{1}{2}$<h<2,最后根据面积和求四边形NQAC的面积为S,并求出t的取值;
(3)存在,设点P(m,n),因为点P在抛物线上,则n=m2-m-2,根据两点距离公式可得:PA2=(m+1)2+n2,PC2=m2+(n+2)2,AC2=5,分三种情况进行讨论:若△PAC为直角三角形时,分以下三种情况:①当∠ACP=90°时,②当∠PAC=90°时,③由图象观察得,当点P在对称轴的右侧时,PA>AC,所以边AC的对角∠APC不可能为90°,分别根据勾股定理列方程求得m和n的值,写出P的坐标;
(4)如图4,根据A和C的坐标直接得出另一矩形顶点D(-1,-2);
如图5,作辅助线,构建直角直角三角形,根据同角的三角函数先求ON的长,再求DF的长和AF的长,所以OF=1-AF,得出点D的坐标,同理,在直角△OCE中,根据面积法先求ME的长,根据三角函数列比例式求OM的长,则可以得到E的坐标,从而得出结论.
解答 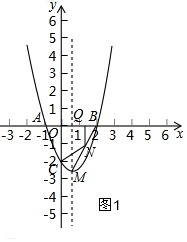 解:(1)设二次函数的解析式为:y=a(x+1)(x-2),
解:(1)设二次函数的解析式为:y=a(x+1)(x-2),
把(0,-2)代入得:-2=a(0+1)(0-2),
a=1,
∴y=(x+1)(x-2)=x2-x-2=(x-$\frac{1}{2}$)2-$\frac{9}{4}$,
∴二次函数的解析式为:y=x2-x-2,顶点M的坐标为($\frac{1}{2}$,-$\frac{9}{4}$);
(2)如图1,设线段BM的解析式为:y=kx+b,
把B(2,0)、M($\frac{1}{2}$,-$\frac{9}{4}$)代入得:$\left\{\begin{array}{l}{2k+b=0}\\{\frac{1}{2}k+b=-\frac{9}{4}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=-3}\end{array}\right.$,
∴线段BM所在的直线解析式为:y=$\frac{3}{2}$x-3,
设N(h,-t),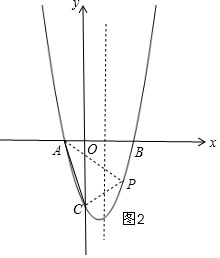
把点N(h,-t)代入y=$\frac{3}{2}$x-3得:$\frac{3}{2}$h-3=-t,
h=2-$\frac{2}{3}$t,其中$\frac{1}{2}$<h<2,
∴S=$\frac{1}{2}$×1×2+$\frac{1}{2}$(2+t)(2-$\frac{2}{3}$t)=-$\frac{1}{3}{t}^{2}$+$\frac{1}{3}$t+3,
则S与t之间的函数关系式为:S=-$\frac{1}{3}{t}^{2}$+$\frac{1}{3}$t+3,
∵顶点M的坐标为($\frac{1}{2}$,-$\frac{9}{4}$),
∴QN的最大值为$\frac{9}{4}$,
∴自变量t的取值范围为0<t<$\frac{9}{4}$;
(3)存在,
设点P(m,n),则n=m2-m-2,
PA2=(m+1)2+n2,PC2=m2+(n+2)2,AC2=5,
若△PAC为直角三角形时,分以下三种情况: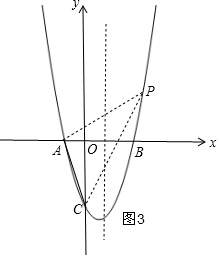
①当∠ACP=90°时,如图2,则PA2=AC2+PC2,
得(m+1)2+n2=m2+(n+2)2+5,
解得:m1=0(舍去),m2=$\frac{3}{2}$,
当m=$\frac{3}{2}$时,n=($\frac{3}{2}$)2-$\frac{3}{2}$-2=-$\frac{5}{4}$,
∴P($\frac{3}{2}$,-$\frac{5}{4}$),
②当∠PAC=90°时,如图3,则PC2=PA2+AC2,
得:m2+(n+2)2=(m+1)2+n2+5,
解得:m1=$\frac{5}{2}$,m2=-1(舍去),
当m=$\frac{5}{2}$时,n=($\frac{5}{2}$)2-$\frac{5}{2}$-2=$\frac{7}{4}$,
∴P($\frac{5}{2}$,$\frac{7}{4}$),
③由图象观察得,当点P在对称轴的右侧时,PA>AC,所以边AC的对角∠APC不可能为90°,
综上所述,点P的坐标为($\frac{3}{2}$,-$\frac{5}{4}$)或($\frac{5}{2}$,$\frac{7}{4}$);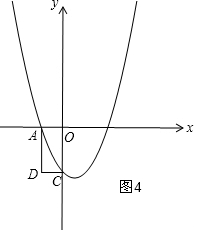
(4)如图4,矩形ADCO,
∵A(-1,0),C(0,-2)
∴D(-1,-2)
如图5,矩形ACED,
过D作DF⊥x轴于F,过E作EM⊥y轴于M,过O作ON⊥AC于N,
sin∠OAC=$\frac{ON}{OA}=\frac{OC}{AC}$,
∴$\frac{ON}{1}=\frac{2}{\sqrt{5}}$,
∴ON=$\frac{2\sqrt{5}}{5}$,
∴AD=ON=$\frac{2\sqrt{5}}{5}$,
cos∠ADF=cos∠OAC=$\frac{DF}{AD}=\frac{OA}{AC}$,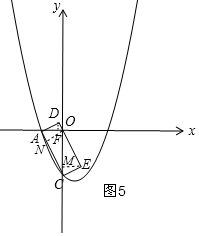
∴$\frac{DF}{\frac{2\sqrt{5}}{5}}$=$\frac{1}{\sqrt{5}}$,
∴DF=$\frac{2}{5}$,
由勾股定理得:AF=$\sqrt{A{D}^{2}-D{F}^{2}}$=$\sqrt{(\frac{2\sqrt{5}}{5})^{2}-(\frac{2}{5})^{2}}$=$\frac{4}{5}$,
∴OF=1-$\frac{4}{5}$=$\frac{1}{5}$,
∴D(-$\frac{1}{5}$,$\frac{2}{5}$),
同理得:E($\frac{4}{5}$,-$\frac{8}{5}$),
综上所述,矩形的未知的顶点坐标是(-1,-2)或(-$\frac{1}{5}$,$\frac{2}{5}$)
或($\frac{4}{5}$,-$\frac{8}{5}$).
点评 本题是二次函数的综合题,主要考查了二次函数解析式的求法,以及顶点坐标的计算,四边形面积的计算,矩形的性质等,综合性较强;当一个三角形是直角三角形时,有两个定点,一个动点,要分三种情况进行讨论,分别让三个顶点为直角顶点时,根据条件进行计算.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
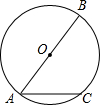 如图,AB是⊙O的直径,AC为⊙O的弦,点D是直径AB上的一点,若OA=5cm,AC=8cm,则CD的长度不可能是( )
如图,AB是⊙O的直径,AC为⊙O的弦,点D是直径AB上的一点,若OA=5cm,AC=8cm,则CD的长度不可能是( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
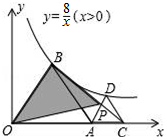 如图,△AOB和△ACD均为正三角形,顶点B、D在双曲线y=$\frac{8}{x}$(x>0)上,线段BC、AD交于点P,则S△OBP=8.
如图,△AOB和△ACD均为正三角形,顶点B、D在双曲线y=$\frac{8}{x}$(x>0)上,线段BC、AD交于点P,则S△OBP=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC三个顶点A、B、C在平面直角坐标系中位置如图所示.将△ABC绕C点顺时针旋转90°,画出旋转后的△A1B1C,并写出A1、B1的坐标.
△ABC三个顶点A、B、C在平面直角坐标系中位置如图所示.将△ABC绕C点顺时针旋转90°,画出旋转后的△A1B1C,并写出A1、B1的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com