
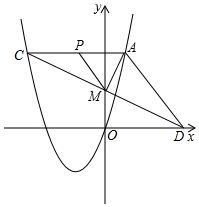
���� ��1���ѵ�B���������˫���߽���ʽ���kֵ���������A�����꣬Ȼ�����ô���ϵ��������κ�������ʽ���
��2��������������ͼ1�У���0��t��5ʱ����PQɨ����ACD��ͼ���ǡ�CPQ����QN��AC��N���ɡ�CPQ�ס�CAM����$\frac{CP}{CA}$=$\frac{QN}{MG}$�����QN���ɣ�����ͼ2�У���5��t��10ʱ����PQɨ����ACD��ͼ�����ı���ACQP������S=S��ACD-S��PQD��⼴�ɣ�
��3�����������A����ֱ��CD�ĶԳƵ�A����x���ϣ�����A����A��P��AC��P����CD��R����ʱPR+AR=PR+RA��=A��P=4�����CP���ɽ�����⣮����ͼ4�У����˶����߶�AD��ʱ��AR��x����P�䣬P��P�����CD�Գƣ���ʱt=7s��
��� �⣺��1����˫����y=$\frac{k}{x}$������B��-2��-2����
��$\frac{k}{-2}$=-2��
���k=4��
��˫���ߵĽ���ʽΪy=$\frac{4}{x}$��
�ߵ�A��������Ϊ4��
��$\frac{4}{x}$=4��
���x=1��
���A��1��4����
�ѵ�A��B����������y=ax2+bx��a��0���ã�
$\left\{\begin{array}{l}{a+b=4}\\{4a-2b=-2}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=1}\\{b=3}\end{array}\right.$��
�������ߵĽ���ʽΪy=x2+3x��
��2����ֱ��AC��x�ᣬA��1��4����
��x2+3x=4��
���x1=1��x2=-4��
���C��������-4��4����
��OD=4��
���D��������4��0����
��ֱ��CD�Ľ���ʽΪy=kx+b��k��0����
��$\left\{\begin{array}{l}{-4k+b=4}\\{4k+b=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$��
��ֱ��CD�Ľ���ʽΪy=-$\frac{1}{2}$x+2��
��x=0ʱ��y=2��
���M��������0��2����
��AC=5��AD=$\sqrt{{3}^{2}+{4}^{2}}$=5��
��AC=AD��
���ACD=��ADC����AC��y����G��
��CG��OD��CG=OD=4��
��$\frac{CG}{OD}$=$\frac{CM}{DM}$=$\frac{GM}{MO}$=1����ACD=��CDO��
���ADC=��CDO��CM=DM��OM=GM=2��
��AM��CD��
����ͼ1�У���0��t��5ʱ����PQɨ����ACD��ͼ���ǡ�CPQ����QN��AC��N��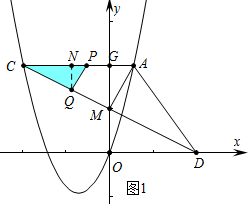
��PQ��AM��
���CPQ=��CAM���ߡ�PCQ=��ACM��
���CPQ�ס�CAM��
��$\frac{CP}{CA}$=$\frac{QN}{MG}$��
��$\frac{t}{5}$=$\frac{QN}{2}$��
��QN=$\frac{2}{5}$t��
��S=$\frac{1}{2}$•CP•QN=$\frac{1}{5}$t2��
����ͼ2�У���5��t��10ʱ����PQɨ����ACD��ͼ�����ı���ACQP��
��PQ��AM��
��$\frac{PQ}{AM}$=$\frac{DP}{DA}$=$\frac{DQ}{DM}$��
��$\frac{PQ}{\sqrt{5}}$=$\frac{10-t}{5}$=$\frac{DQ}{2\sqrt{5}}$��
��PQ=$\frac{\sqrt{5}}{5}$��10-t����DQ=$\frac{2\sqrt{5}}{5}$��10-t����
��S=S��ACD-S��PQD=$\frac{1}{2}$��4$\sqrt{5}$��$\sqrt{5}$-$\frac{1}{2}$��$\frac{\sqrt{5}}{5}$��10-t����$\frac{2\sqrt{5}}{5}$��10-t��=-$\frac{1}{5}$t2+4t-10��
����������S=$\left\{\begin{array}{l}{\frac{1}{5}{t}^{2}}&{��0��t��5��}\\{-\frac{1}{5}{t}^{2}+4t-10}&{��5��t��10��}\end{array}\right.$��
��3�����ڣ�����ͼ3�У�
�ɣ�2����֪����CDA=��CDO��
���A����ֱ��CD�ĶԳƵ�A����x���ϣ�����A����A��P��AC��P����CD��R����ʱPR+AR=PR+RA��=A��P=4��
��DA=DA��=5��
��OA��=PG=1��
��CP=3��
��t=3sʱ���߶�CD����һ����R����AR+RPΪ4��
����ͼ4�У����˶����߶�AD��ʱ��AR��x����P�䣬P��P�����CD�Գƣ���ʱt=7s��
����������t=3s��7sʱ��AR+RPΪ4��
���� �����Ƕ��κ����ۺ����͡�����ϵ���������ɶ�����Ӧ�á��Լ������ε���������������ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ��ѧ���÷������۵�˼��˼�����⣬ѧ�����öԳƽ���й����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 36.2��103m | B�� | 3.62��103m | C�� | 0.362��104m | D�� | 3.62��104m |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��l1����ƽ��1����λ | B�� | ��l1����ƽ��1����λ | ||
| C�� | ��l1����ƽ��2����λ | D�� | ��l1����ƽ��1����λ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com