
【题目】如图,等边△ABC放置在平面直角坐标系中,已知A(0,0)、B(2,0),反比例函数的图象经过点C.
(1)求点C的坐标及反比例函数的解析式.
(2)如果将等边△ABC向上平移n个单位长度,使点B恰好落在双曲线上,求n的值.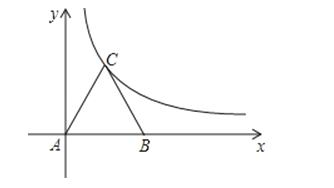
【答案】解:(1)过点C作CD⊥x轴,垂足为D,如图,设反比例函数的解析式为![]() ,
,
∵A(0,0)、B(2,0),
∴AB=2,
∵△ABC是等边三角形,
∴AC=AB=2,∠CAB=60°,
∴AD=1,CD=ACsin60=2×![]() =
=![]() ,
,
∴点C坐标为(1,![]() ),
),
∵反比例函数的图象经过点C,
∴k=1×![]() =
=![]() ,
,
∴反比例函数的解析式![]() ;
;
(2)∵将等边△ABC向上平移n个单位,则平移后B点坐标为(2,n),而平移后的点B恰好落在双曲线上,
∴2n=![]() ,
,
∴n=![]() .
.
【解析】(1)过点C作CD⊥x轴,垂足为D,如图,根据等边三角形的性质得到AC=AB=2,∠CAB=60°,AD=1,再利用三角函数可计算出CD![]() =
=![]() , 则点C坐标为(1,
, 则点C坐标为(1,![]() ),然后利用待定系数法求反比例函数解析式;
),然后利用待定系数法求反比例函数解析式;
(2)根据点平移规律得到平移后B点坐标为(2,n),然后根据反比例函数图象上点的坐标特征得到2n=![]() , 再解方程即可.
, 再解方程即可.
【考点精析】利用反比例函数的性质对题目进行判断即可得到答案,需要熟知性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.


科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小丁在研究数学问题时遇到一个定义:对于排好顺序的三个数: ![]() ,称为数列
,称为数列![]() .计算
.计算![]() ,
, ![]() ,
, ![]() 将这三个数的最小值称为数列
将这三个数的最小值称为数列![]() 的价值.例如,对于数列2,﹣1,3,因为
的价值.例如,对于数列2,﹣1,3,因为![]() ,
, ![]() ,
, ![]() ,所以数列2,﹣1,3的价值为
,所以数列2,﹣1,3的价值为![]() .
.
小丁进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值.如数列﹣1,2,3的价值为![]() ;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为
;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列﹣4,﹣3,2的价值为 ;
(2)将“﹣4,﹣3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的价值的最小值为 ,取得价值最小值的数列为 (写出一个即可);
(3)将2,﹣9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的价值的最小值为1,则a的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件120元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量![]() (件)是销售单价
(件)是销售单价![]() (元)的函数,并且满足如下对应值表:
(元)的函数,并且满足如下对应值表:
销售单价 | 130 | 140 | 145 |
销售量 | 110 | 100 | 95 |
(1)求![]() 与
与![]() 的函数表达式;
的函数表达式;
(2)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于 2000元,试确定销售单价![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将多项式﹣y2+2y3+1﹣y按照字母y升幂排列正确的是( )
A.2y3﹣y2﹣y+1
B.﹣y﹣y2+2y3+1
C.1+2y3﹣y2﹣y
D.1﹣y﹣y2+2y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每格为1个单位的正方形网格中建立直角坐标系,反比例函数y=![]() 的图象经过格点A.
的图象经过格点A.
(1)请写出点A的坐标、反比例函数y=![]() 的解析式;
的解析式;
(2)若点B(m,y1)、C(n,y2)(2<m<n)都在函数y=![]() 的图象上,试比较y1与y2的大小.
的图象上,试比较y1与y2的大小.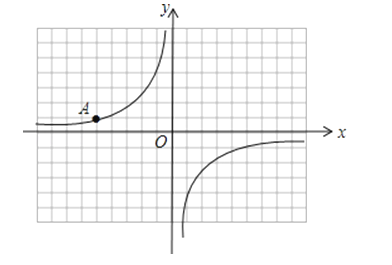
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 两条射线组成的图形叫做角
B. 有公共端点的两条线段组成的图形叫做角
C. 角可以看做是由一条射线绕着它的端点旋转而形成的图形
D. 角可以看做是由一条线段绕着它的端点旋转而形成的图形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com