
【题目】如图,等腰△ABC内接于⊙O,AB=AC=4![]() ,BC=8,则⊙O的半径为___________.
,BC=8,则⊙O的半径为___________.

【答案】5cm
【解析】
作AD⊥BC于D,根据等腰三角形的性质得BD=CD=![]() BC=4,再利用三角形外心的定义得到△ABC的外接圆的圆心在AD上,连结OB,设⊙O的半径为r,利用勾股定理,在Rt△ABD中计算出AD=8,然后在Rt△OBD中得到42+(8-r)2=r2,再解关于r的方程即可;
BC=4,再利用三角形外心的定义得到△ABC的外接圆的圆心在AD上,连结OB,设⊙O的半径为r,利用勾股定理,在Rt△ABD中计算出AD=8,然后在Rt△OBD中得到42+(8-r)2=r2,再解关于r的方程即可;
解:
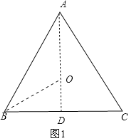
如图1,作AD⊥BC于D,
∵AB=AC,
∴BD=CD=![]() BC=4,
BC=4,
∴△ABC的外接圆的圆心在AD上,
连结OB,设⊙O的半径为r,
在Rt△ABD中,∵AB=4![]() ,BD=4,
,BD=4,
∴AD=![]() =8,
=8,
在Rt△OBD中,OD=AD-OA=8-r,OB=r,BD=4,
∴42+(8-r)2=r2,解得r=5,
即△ABC的外接圆的半径为5;


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
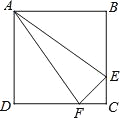
A. 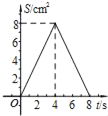 B.
B. 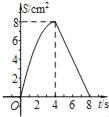
C. 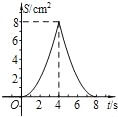 D.
D. 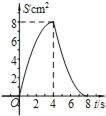
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=∠ACB。

(1)若D为BC边上一点,E为直线AC上一点,且∠ADE=∠AED.求证:∠BAD=2∠CDE;
(2)如图,若D在BC的反向延长线上,其它条件不变,(1)中的结论是否仍然成立?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了三角形全等的判定方法(即SSS,SAS,ASA,AAS)和直角三角形全等的判定方法(即HL)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
(初步思考)
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后对∠B进行分类,可以分为“∠B是直角、钝角、锐角”三种情况进行探究.
(深入探究)
第一种情况:当∠B为锐角时,△ABC和△DEF不一定全等.
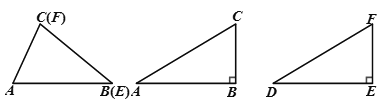
(1)如图,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你用尺规在图中确定点D,使△DEF和△ABC不全等(不写作法,保留作图痕迹);
第二种情况:当∠B为直角时,△ABC≌△DEF.
(2)如图,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据____,可以知道Rt△ABC≌Rt△DEF.
第三种情况:当∠B为钝角时,△ABC≌△DEF.
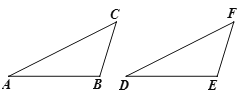
(3)如图,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角,求证:△ABC≌△DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
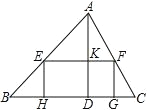
【题目】如图,锐角△ABC 中,BC=12,BC 边上的高 AD=8,矩形 EFGH 的边 GH在 BC 上,其余两点 E、F 分别在 AB、AC 上,且 EF 交 AD 于点 K
(1) 求![]() 的值
的值
(2) 设 EH=x,矩形 EFGH 的面积为 S
① 求 S 与 x 的函数关系式
② 请直接写出 S 的最大值
查看答案和解析>>
科目:初中数学 来源: 题型:
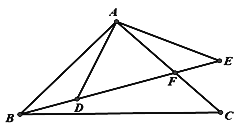
【题目】如图,点B、D、E在一条直线上,BE与AC相交于点F,且![]()
⑴求证:△ABC∽△ADE;
⑵求证:∠BAD=∠CAE;
⑶若∠BAD=18°,求∠EBC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com