
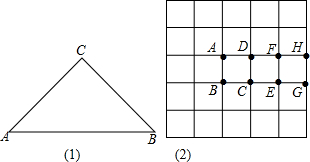
分析 (1)如图(1),过C作CD⊥AB于D,得到∠ADC=∠BDC=90°,推出Rt△ACD≌Rt△BCD,于是得到∠A=∠B,然后根据三角形的内角和即可得到结论;
(2)如图(2),连接AC根据正方形的性质得到∠ACB=45°,设四边形ABCD、DCEF、FEGH的边长为1,推出△ACE∽△GCA,得到∠AEC=∠CAG,然后根据三角形的外角的性质即可得到结论.
解答  解:(1)如图(1),过C作CD⊥AB于D,
解:(1)如图(1),过C作CD⊥AB于D,
∴∠ADC=∠BDC=90°,
在Rt△ACD与Rt△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{CD=CD}\end{array}\right.$,
∴Rt△ACD≌Rt△BCD,
∴∠A=∠B,
∵∠ACB=90°,
∴∠A=∠B=45°;
(2)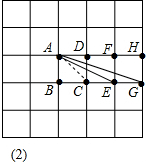 如图(2),连接AC,
如图(2),连接AC,
∵四边形ABCD、DCEF、FEGH均为边长都相等的正方形,
∴∠ACB=45°,
设四边形ABCD、DCEF、FEGH的边长为1,
∴AC=$\sqrt{2}$,
∴$\frac{AC}{CG}=\frac{\sqrt{2}}{2}$,$\frac{CE}{AC}$=$\frac{\sqrt{2}}{2}$,
∵∠ACE=∠GCA,
∴△ACE∽△GCA,
∴∠AEC=∠CAG,
∵∠ACB=∠CAG+∠AGB=∠AEB+∠AGB,
∴∠AEB+∠AGB=45°.
故答案为:45.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,等腰直角三角形的性质,正确作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
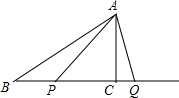 如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=acm,动点P,Q分别从点B,点C开始沿着射线BC运动,点P的速度为2cm/s,点Q的速度为1cm/s.两点同时出发,当点P追上点Q时两点都停止运动,设运动时间为t秒.
如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=acm,动点P,Q分别从点B,点C开始沿着射线BC运动,点P的速度为2cm/s,点Q的速度为1cm/s.两点同时出发,当点P追上点Q时两点都停止运动,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$×4$\sqrt{2}$=12$\sqrt{2}$ | B. | $\sqrt{(-9)×(-25)}=\sqrt{9}×\sqrt{-25}=(-3)×(-5)=15$ | ||
| C. | -3$\sqrt{\frac{2}{3}}$=$\sqrt{{{(-3)}^2}×\frac{2}{3}}$=6 | D. | $\sqrt{{{13}^2}-{{12}^2}}=\sqrt{(13+12)(13-12)}$=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,抛物线y=ax2+bx+c与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则下列说法不正确的是( )
如图,抛物线y=ax2+bx+c与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则下列说法不正确的是( )| A. | 方程ax2+bx+c=0的两根为x1=-1,x2=2 | |
| B. | 抛物线y=ax2+bx+c与直线y=2x+4无交点 | |
| C. | 当y>0时,-1<x<2 | |
| D. | 当y>2时,$\frac{1}{2}$<x<1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (-0.5,1) | C. | (-1,-2) | D. | (2,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{4}{3}$ | C. | 2或$\frac{4}{3}$ | D. | 2或-$\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com