
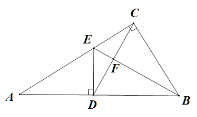
【题目】如图,在Rt△ABC中,∠ACB=![]() ,D是AB边上的一点,过D作DE⊥AB交AC于点E,BC=BD,连结CD交BE于点F.
,D是AB边上的一点,过D作DE⊥AB交AC于点E,BC=BD,连结CD交BE于点F.
(1)求证:CE=DE;
(2)若点D为AB的中点,求∠AED的度数.
【答案】(1)证明见解析;(2)60°;
【解析】
(1)直接证明Rt△DEB≌Rt△CEB,即可解决问题.
(2)首先证明△ADE≌△BDE,进而证明∠AED=∠DEB=∠CEB,即可解决问题.
(1)∵DE⊥AB,∠ACB=![]()
∴△BCE与△BDE都是直角三角形.
在Rt△BCE与Rt△BDE中
![]()
∴Rt△BCE≌Rt△BDE(HL)
∴CE=DE
(2)∵DE⊥AB,
∴∠ADE=∠BDE=![]()
∵点D为AB的中点,
∴AD=BD
又∵DE=DE,
∴△ADE≌△BDE,
∴∠AED=∠DEB
∵△BCE≌△BDE,
∴∠CEB=∠DEB
∴∠AED=∠DEB=∠CEB,
∵∠AED+∠DEB+∠CEB=![]() ,
,
∴∠AED=![]()


科目:初中数学 来源: 题型:
【题目】如图,已知 ![]() 中,
中,![]() 厘米,
厘米,![]() ,
,![]() 厘米,点
厘米,点 ![]() 为
为 ![]() 的中点.如果点
的中点.如果点 ![]() 在线段
在线段 ![]() 上以
上以 ![]() 厘米/秒的速度由
厘米/秒的速度由 ![]() 点向
点向 ![]() 点运动.同时,点
点运动.同时,点 ![]() 在线段
在线段 ![]() 上由
上由 ![]() 点以
点以 ![]() 厘米/秒的速度向
厘米/秒的速度向 ![]() 点运动.设运动的时间为
点运动.设运动的时间为 ![]() 秒.
秒.

(1)直接写出:
①BD=_______厘米; ②BP=________厘米;
③CP=_______厘米; ④CQ=_______厘米;
(可用含 ![]() 、a的代数式表示)
、a的代数式表示)
(2)若以 ![]() ,
,![]() ,
,![]() 为顶点的三角形和以
为顶点的三角形和以 ![]() ,
,![]() ,
,![]() 为顶点的三角形全等,试求
为顶点的三角形全等,试求 ![]() 、t的值;
、t的值;
(3)若点 ![]() 以(
以(![]() )中的运动速度从点
)中的运动速度从点 ![]() 出发,点
出发,点 ![]() 以原来的运动速度从点
以原来的运动速度从点 ![]() 同时出发,都逆时针沿
同时出发,都逆时针沿 ![]() 三边运动.设运动的时间为
三边运动.设运动的时间为 ![]() 秒;直接写出t= 秒时点
秒;直接写出t= 秒时点 ![]() 与点
与点 ![]() 第一次相遇.
第一次相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是( )
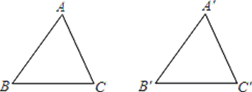
A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
查看答案和解析>>
科目:初中数学 来源: 题型:
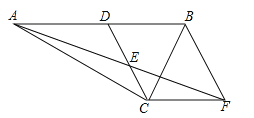
【题目】已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB叫AE的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若∠DCF=120°,DE=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架云梯AB的长25 m,斜靠在一面墙上,梯子靠墙的一端A距地面距离AC为24 m.
(1)这个梯子底端B离墙的距离BC有多少米?
(2)如果梯子的顶端下滑了4 m,那么梯子的底部在水平方向也滑动了4 m吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生上学带手机的现象越来越受到社会的关注,为此媒体记者随机调查了某校若干名学生上学带手机的目的,分为四种类型:A接听电话;B收发短信;C查阅资料;D游戏聊天.并将调查结果绘制成图1和图2的统计图(不完整),请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生.
(2)将图1、图2补充完整;
(3)现有4名学生,其中A类两名,B类两名,从中任选2名学生,求这两名学生为同一类型的概率(用列表法或树状图法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=13,AC=5,BC边上的中线AD=6,点E在AD的延长线上,且AD=DE.
(1)试判断△ABE的形状并说明理由;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习成为现代人的时尚,某市有关部门统计了最近6个月到图书馆的读者的职业分布情况,并做了下列两个不完整的统计图. 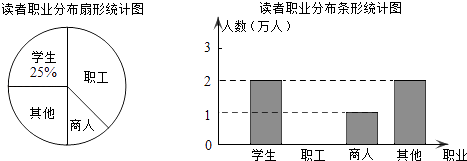
(1)在统计的这段时间内,共有万人次到图书馆阅读,其中商人占百分比为%;
(2)将条形统计图补充完整;
(3)若5月份到图书馆的读者共28000人次,估计其中约有多少人次读者是职工?
查看答案和解析>>
科目:初中数学 来源: 题型:
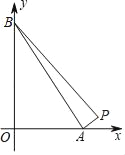
【题目】由点P(14,1),A(a,0),B(0,a)确定的△PAB的面积为18.
(1)如图,若0<a<14,求a的值.
(2)如果a>14,请画图并求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com