
【题目】某篮球运动员去年共参加![]() 场比赛,其中
场比赛,其中![]() 分球的命中率为
分球的命中率为![]() ,平均每场有
,平均每场有![]() 次
次![]() 分球未投中.
分球未投中.
![]() 该运动员去年的比赛中共投中多少个
该运动员去年的比赛中共投中多少个![]() 分球?
分球?
![]() 在其中的一场比赛中,该运动员
在其中的一场比赛中,该运动员![]() 分球共出手
分球共出手![]() 次,小明说,该运动员这场比赛中一定投中了
次,小明说,该运动员这场比赛中一定投中了![]() 个
个![]() 分球,你认为小明的说法正确吗?请说明理由.
分球,你认为小明的说法正确吗?请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法:
①两个数互为倒数,则它们的乘积为![]() ;②若
;②若![]() ,
,![]() 互为相反数,则
互为相反数,则![]() ;
;
③![]() 个有理数相乘,如果负因数的个数为奇数个,则积为负;④若
个有理数相乘,如果负因数的个数为奇数个,则积为负;④若![]() ,则
,则![]() .其中正确的个数为( )
.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A点的初始位置位于数轴上表示1的点,现对A点做如下移动:第1次向左移动3个单位长度至B点,第2次从B点向右移动6个单位长度至C点,第3次从C点向左移动9个单位长度至D点,第4次从D点向右移动12个单位长度至E点,…,依此类推.这样第_____次移动到的点到原点的距离为2018.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线AB:y=5x﹣5与x轴交于点A,与y轴交于点B,点C与点B关于原点O对称,抛物线y=ax2+bx+c的对称轴为直线x=3且过点A和C. 
(1)求点A和点C的坐标;
(2)求抛物线y=ax2+bx+c的解析式;
(3)若抛物线y=ax2+bx+c的顶点为D,且在x轴上存在点P使得△DAP的面积为6,直接写出满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个“有理数转换器”(箭头是指有理数进入转换器后的路径,方框是对进入的数进行转换的转换器)
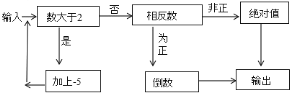
![]() 当小明输入
当小明输入![]() ;
;![]() ;
;![]() 这三个数时,这三次输入的结果分别是多少?
这三个数时,这三次输入的结果分别是多少?
![]() 你认为当输入什么数时,其输出的结果是
你认为当输入什么数时,其输出的结果是![]() ?
?
![]() 你认为这的“有理数转换器”不可能输出什么数?
你认为这的“有理数转换器”不可能输出什么数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】石头剪子布,又称“猜丁壳”,是一种起源于中国流传多年的猜拳游戏.游戏时的各方每次用一只手做“石头”、“剪刀”、“布”三种手势中的一种,规定“石头”胜“剪刀”、“剪刀”胜“布”、“布”胜“石头”.两人游戏时,若出现相同手势,则不分胜负游戏继续,直到分出胜负,游戏结束.三人游戏时,若三种手势都相同或都不相同,则不分胜负游戏继续;若出现两人手势相同,则视为一种手势与第三人所出手势进行对决,此时,参照两人游戏规则.例如甲、乙二人同时出石头,丙出剪刀,则甲、乙获胜.假定甲、乙、丙三人每次都是随机地做这三种手势,那么:
(1)请你用画树状图或列表的方式,求出一次游戏中甲、乙两人出第一次手势时,不分胜负的概率;
(2)请直接写出一次游戏中甲、乙、丙三人出第一次手势时,不分胜负的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACD和△BCE中,AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为 __________.
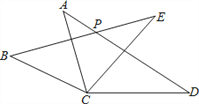
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com