
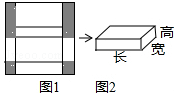
 图1是边长为30的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知长方体的宽是高的2倍,求该长方体盒子的体积和表面积.
图1是边长为30的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知长方体的宽是高的2倍,求该长方体盒子的体积和表面积. 分析 设长方体的高为x,则长方体的宽为2x,长方体的长为(30-2x),观察图1结合正方形的边长为30,即可得出关于x的一元一次方程,解之即可得出x的值,进而即可得出长方体的长和宽,再套用长方体的体积和表面积公式即可求出结论.
解答 解:设长方体的高为x,则长方体的宽为2x,长方体的长为(30-2x),
根据题意得:2x+x+2x+x=30,
解得:x=5,
∴2x=10,30-2x=20.
∴长方体的体积为20×10×5=1000;
长方体的表面积为2×(20×10+20×5+10×5)=700.
答:该长方体盒子的体积为1000,表面积为700.
点评 本题考查了一元一次方程的应用以及展开图折叠成几何体,根据长方体宽和高之间的关系,列出一元一次方程是解题的关键.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:选择题
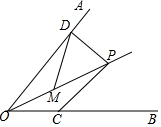 如图,已知点P是∠AOB平分线上一点,∠AOB=60°,PD⊥OA,垂足为D,M是OP上一点,连接MD,MD=MP,OM=4cm,点C是OB上一个动点,则PC的最小值为( )
如图,已知点P是∠AOB平分线上一点,∠AOB=60°,PD⊥OA,垂足为D,M是OP上一点,连接MD,MD=MP,OM=4cm,点C是OB上一个动点,则PC的最小值为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 1cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2012个点的横坐标为( )
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2012个点的横坐标为( )| A. | 40 | B. | 45 | C. | 50 | D. | 55 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
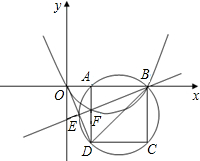 如图,在平面直角坐标系中,已知点A(m,0)(0<m<$\sqrt{2}$),B(2$\sqrt{2}$,0),以AB为边在x轴下方作正方形ABCD,点E是线段OD与正方形ABCD的外接圆的交点,连接BE与AD相交于点F.
如图,在平面直角坐标系中,已知点A(m,0)(0<m<$\sqrt{2}$),B(2$\sqrt{2}$,0),以AB为边在x轴下方作正方形ABCD,点E是线段OD与正方形ABCD的外接圆的交点,连接BE与AD相交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com