
 如图是一个中心对称图形,A为对称中心,若∠C=90°,AC=$\frac{\sqrt{3}}{3}$,BC=1,则BB′长为( )
如图是一个中心对称图形,A为对称中心,若∠C=90°,AC=$\frac{\sqrt{3}}{3}$,BC=1,则BB′长为( )| A. | 4 | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
分析 先根据∠C=90°,AC=$\frac{\sqrt{3}}{3}$,BC=1,求出边BA的长度,再根据该图形为中心对称图形得出BA=B′A,然后由BB′=BA+B′A求解即可.
解答 解:∵∠C=90°,AC=$\frac{\sqrt{3}}{3}$,BC=1,
∴根据勾股定理可得:BA=$\sqrt{{{AC}^{2}+BC}^{2}}$=$\sqrt{\frac{1}{3}+1}$=$\frac{2\sqrt{3}}{3}$,
∵该图形为中心对称图形,
∴BA=B′A,
∴BB′=BA+B′A=2×$\frac{2\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$.
故选D.
点评 本题考查了中心对称图形和勾股定理的知识,解答本题的关键在于熟练掌握中心对称图形的概念和勾股定理的运算法则.


科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,AE=4,BC=8,有下列结论:
如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,AE=4,BC=8,有下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△AOC中,OA=OC,点B是AO延长线上一点,OD平分∠AOC交AC于点D,OM平分∠COB,CF⊥OM于点F.
如图,在△AOC中,OA=OC,点B是AO延长线上一点,OD平分∠AOC交AC于点D,OM平分∠COB,CF⊥OM于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
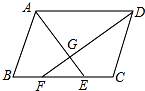 如图,在?ABCD中,∠BAD、∠ADC的平分线AE、DF分别交BC于点E、F,AE与DF相交于点G.
如图,在?ABCD中,∠BAD、∠ADC的平分线AE、DF分别交BC于点E、F,AE与DF相交于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com