
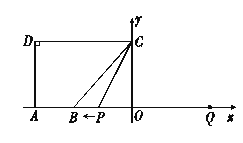
【题目】如图,![]() 点
点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为![]() 秒.
秒.
(1)点![]() 的坐标是 ;
的坐标是 ;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)以点![]() 为圆心,
为圆心,![]() 为半径的
为半径的![]() 随点
随点![]() 的运动而变化,当
的运动而变化,当![]() 与四边形
与四边形![]() 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求![]() 的值.
的值.
【答案】(1)、(0,6);(2)、![]() 或
或![]() ;(3)、1或7或
;(3)、1或7或![]()
【解析】
试题分析:(1)、根据题意得出点C的坐标;(2)、本题分两种情况进行计算,当点P在点B右侧,根据题意得出∠PCO=30°,则OP=t-7,PC=2(t-7),根据Rt△POC的勾股定理得出t的值,当点P在点B左侧,用同样的方法得出t的值;(3)、与四边形相切时,分三种情况进行讨论,即与BC相切,与CD相切,与AD相切.
试题解析:(1)点![]() 的坐标为(0,6);
的坐标为(0,6);
(2)当点![]() 在点
在点![]() 右侧时,如图2.
右侧时,如图2.
当![]() ,得
,得![]() .OP=t-7,则PC=2(t-7),在Rt△POC中,
.OP=t-7,则PC=2(t-7),在Rt△POC中, ![]()
故![]() ,此时
,此时![]() (舍去负值)
(舍去负值)
当点![]() 在点
在点![]() 左侧时,如图3,由
左侧时,如图3,由![]() ,
,
得![]() ,PC=2CO=12,故
,PC=2CO=12,故![]() .
.
此时![]() .
.![]() 的值为
的值为![]() 或
或![]() ;
;
(3)由题意知,若![]() 与四边形
与四边形![]() 的边相切,有以下三种情况:
的边相切,有以下三种情况:
①当![]() 与
与![]() 相切于点
相切于点![]() 时,有
时,有![]() ,从而
,从而![]()
得到![]() . 此时
. 此时![]() .
.
②当![]() 与
与![]() 相切于点
相切于点![]() 时,有
时,有![]() ,即点
,即点![]() 与点
与点![]() 重合,此时
重合,此时![]() .
.
③当![]() 与
与![]() 相切时,由题意,
相切时,由题意,![]() ,
,
![]() 点
点![]() 为切点,如图4.
为切点,如图4.![]() .
.
于是![]() .解出
.解出![]() .
.
![]() 的值为1或7或
的值为1或7或![]() .
.




科目:初中数学 来源: 题型:
【题目】完成证明并写出推理根据: 已知,如图,∠1=132°,∠ACB=48°,∠2=∠3,FH⊥AB于H.
求证:CD⊥AB.
证明:∵∠1=132°,∠ACB=48°,
∴∠1+∠ACB=180°
∴DE∥BC
∴∠2=()
又∵∠2=∠3
∴∠3=∠DCB
∴HF∥()
∴∠CDB= . ()
又∵FH⊥AB,
∴∠FHB=()
∴∠CDB=°.
∴CD⊥AB.()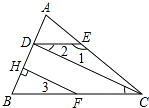
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种零件,标明要求是φ:20±0.02 mm(φ表示直径,单位:毫米),经检查,一个零件的直径是19.9 mm,该零件(填“合格”或“不合格”).
查看答案和解析>>
科目:初中数学 来源: 题型:
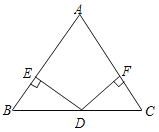
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
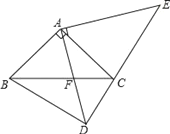
【题目】如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E在同一直线上,连接BD.
(1)求证:BD=EC;
(2)BD与CE有何位置关系?请证你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com