
【题目】如图,在ABCD中,对角线AC,BD相交于点O,过点O作BD的垂线与边AD,BC分别交于点E,F,连接BE交AC于点K,连接DF.
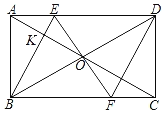
(1)求证:四边形EBFD是菱形;
(2)若BK=3EK,AE=4,求四边形EBFD的周长.
【答案】(1)见解析;(2)32
【解析】
(1)四边形ABCD是平行四边形,可以证明△DEO≌△BFO,可得OE=OF,从而四边形EBFD是平行四边形,根据EF⊥BD,进而可得平行四边形EBFD是菱形;
(2)证明△AEK∽△CBK,对应边成比例可得BC=12,进而求出DE的长,可得菱形的周长.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠EDO=∠FBO,
OB=OD,
∠EOF=∠FOB,
∴△DEO≌△BFO(ASA),
∴OE=OF,
∴四边形EBFD是平行四边形,
∵EF⊥BD,
∴平行四边形EBFD是菱形;
(2)∵AE//BC,
∴△AEK∽△CBK,
∴![]() =
=![]() ,
,
∵BK=3EK,AE=4,
∴![]() =
=![]() ,
,
∴BC=12,
∴AD=BC=DE+AE=DE+4=12,
∴DE=8,
∴菱形EBFD的周长为4DE=32.
答:四边形EBFD的周长为32.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点到直线的距离即为点到直线的垂线段的长.

(1)如图1,取点M(1,0),则点M到直线l:y=![]() x﹣1的距离为多少?
x﹣1的距离为多少?
(2)如图2,点P是反比例函数y=![]() 在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=
在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=![]() ?若存在,求出点P的坐标,若不存在,请说明理由.
?若存在,求出点P的坐标,若不存在,请说明理由.
(3)如图3,若直线y=kx+m与抛物线y=x2﹣4x相交于x轴上方两点A、B(A在B的左边).且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离最大时,直线y=kx+m的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
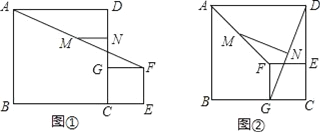
【题目】如图①,C为线段BE上的一点,分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN
(1)线段MN和GD的数量关系是_____,位置关系是_____;
(2)将图①中的正方形CEFG绕点C逆时针旋转90°,其他条件不变,如图②,(1)的结论是否成立?说明理由;
(3)已知BC=7,CE=3,将图①中的正方形CEFG绕点C旋转一周,其他条件不变,直接写出MN的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级学生参加社会实践活动情况,随机调查了本校部分八年级学生在第一学期参加社会实践活动的天数,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
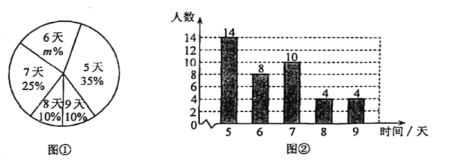
(1)本次接受随机抽样调查的学生人数为 ,图①中的![]() 的值为 ;
的值为 ;
(2)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(3)若该校八年级学生有![]() 人,估计参加社会实践活动时间大于
人,估计参加社会实践活动时间大于![]() 天的学生人数.
天的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
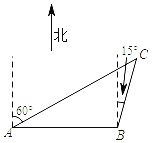
【题目】在一次综合社会实践活动中,小东同学从A处出发,要到A地北偏东60°方向的C处,他先沿正东方向走了4千米到达B处,再沿北偏东15°方向走,恰能到达目的地C,如图所示,则A、C两地相距__千米.(结果精确到0.1千米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线L:y=kx+2k(k>0)与x轴交于点A,与y轴交于点B,与函数![]() (x>0)的图象的交点P位于第一象限.
(x>0)的图象的交点P位于第一象限.
(1)若点P的坐标为(1,6),
①求m的值及点A的坐标;
②![]() =_________;
=_________;
(2)直线h:y=2kx-2与y轴交于点C,与直线L1交于点Q,若点P的横坐标为1,
①写出点P的坐标(用含k的式子表示);
②当PQ≤PA时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
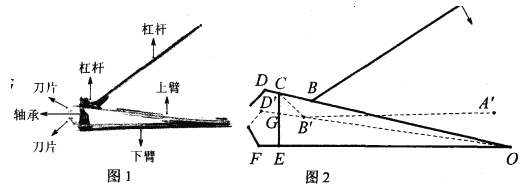
【题目】图1是一种指甲剪.该指甲剪利用杠杆原理操作,使用者只需施力按压柄的末端,便可轻易透过锋利的前端刀片剪断指甲,它被按压后示意图如图2所示,上下臂![]()
![]() 杠杆
杠杆![]() 轴承
轴承![]() ,未使用指甲剪时,点
,未使用指甲剪时,点![]() 在
在![]() 上,且
上,且![]() 比
比![]() 长
长![]() ,则
,则![]() 的长为________
的长为________![]() ;使用指甲剪时,下压点
;使用指甲剪时,下压点![]() ,当
,当![]() 时,两刀片咬合,
时,两刀片咬合,![]() 绕点
绕点![]() 按逆时针方向旋转到
按逆时针方向旋转到![]() 的位置,则
的位置,则![]() 与
与![]() 的交点从开始到结束时移动的距离
的交点从开始到结束时移动的距离![]() 为_______
为_______![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
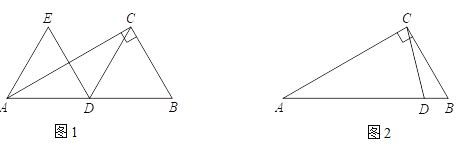
【题目】在△ABC中,∠ACB=90°,∠CAB=30°,点D在AB上,连接CD,并将CD绕点D逆时针旋转60°得到DE,连接AE.
(1)如图1,当点D为AB中点时,直接写出DE与AE长度之间的数量关系;
(2)如图2,当点D在线段AB上时,
① 根据题意补全图2;
② 猜想DE与AE长度之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com