
【题目】如图,将△ABC沿射线BC平移得到△A′B′C′,使得点A′落在∠ABC的平分线BD上,连接AA′,AC′.
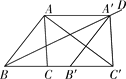
(1)判断四边形ABB′A′的形状,并证明;
(2)在△ABC中,AB=6,BC=4,若AC′⊥A′B′,求四边形ABB′A′的面积.
【答案】(1)四边形ABB′A′是菱形,证明见解析;(2)![]()
【解析】
(1)先根据平移的性质得出四边形ABB′A′是平行四边形,则有∠AA′B=∠A′BC,再通过角平分线的定义通过等量代换得出∠AA′B=∠A′BA,则有AB=AA′,则可证明![]() 是菱形;
是菱形;
(2)过点A作AF⊥BC于点F,设AC′与A′B′交于点E,由AB∥A′B′可得出∠BAC′=∠B′EC′=90°,在Rt△ABC′中利用勾股定理求出AC′的长度,然后利用等面积法求出AF的长度,最后利用S菱形ABB′A′=BB′·AF即可求出答案.
解:(1)四边形ABB′A′是菱形.
证明如下:由平移得AB∥A′B′,AB=A′B′,
∴四边形ABB′A′是平行四边形,
∴∠AA′B=∠A′BC.
∵BA′平分∠ABC,
∴∠ABA′=∠A′BC.
∴∠AA′B=∠A′BA.
∴AB=AA′.
∴![]() 是菱形;
是菱形;
(2)如解图,过点A作AF⊥BC于点F,设AC′与A′B′交于点E.
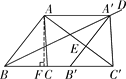
由(1)得BB′=BA=6.
由平移得△A′B′C′≌△ABC,
∴B′C′=BC=4.
∴BC′=10.
∵AC′⊥A′B′,
∴∠B′EC′=90°.
∵AB∥A′B′,
∴∠BAC′=∠B′EC′=90°.
在Rt△ABC′中,AC′=![]() =8.
=8.
∵S△ABC′=![]() AB·AC′=
AB·AC′=![]() BC′·AF,
BC′·AF,
∴AF=![]() =
=![]() .
.
∴S菱形ABB′A′=BB′·AF=![]() .
.
即四边形SABB′A′的面积是![]() .
.


科目:初中数学 来源: 题型:
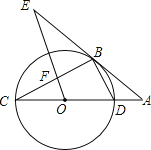
【题目】如图,CD是⊙O的直径,点B在⊙O上,连接BC、BD,直线AB与CD的延长线相交于点A,AB2=ADAC,OE∥BD交直线AB于点E,OE与BC相交于点F.
(1)求证:直线AE是⊙O的切线;
(2)若⊙O的半径为3,cosA=![]() ,求OF的长.
,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与坐标轴分别交于
与坐标轴分别交于![]() ,
,![]() ,
,![]() 三点,连接
三点,连接![]() ,
,![]() .
.
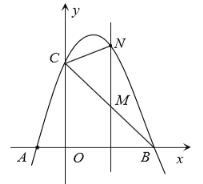
(1)直接写出![]() ,
,![]() ,
,![]() 三点的坐标;
三点的坐标;
(2)点![]() 是线段
是线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,连接
,连接![]() .若点
.若点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好在
恰好在![]() 轴上,求出点
轴上,求出点![]() 的坐标;
的坐标;
(3)在平面内是否存在一点![]() ,使
,使![]() 关于点
关于点![]() 的对称
的对称![]() (点
(点![]() ,
,![]() ,
,![]() 分别是点
分别是点![]() ,
,![]() ,
,![]() 的对称点)恰好有两个顶点落在该抛物线上?若存在,求出点
的对称点)恰好有两个顶点落在该抛物线上?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,G为CD边中点,连接AG并延长,分别交对角线BD于点F,交BC边延长线于点E.若FG=2,则AE的长度为( )
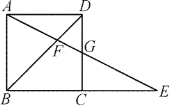
A. 6B. 8
C. 10D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的出行方式,随机从全校2000名学生中抽取了300名学生进行调查,并根据调查结果绘制如下条形统计图,下列说法不正确的是( )
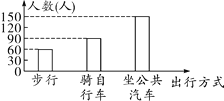
A.样本中步行人数最少
B.本次抽样的样本容量是300
C.样本中坐公共汽车的人数占调查人数的50%
D.全校步行、骑自行车的人数的总和与坐公共汽车的人数一定相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教育部基础教育司负责人解读“2020新中考”时强调要注重学生分析与解决问题的能力,要增强学生的创新精神和综合素质.王老师想尝试改变教学方法,将以往教会学生做题改为引导学生会学习.于是她在菱形的学习中,引导同学们解决菱形中的一个问题时,采用了以下过程(请解决王老师提出的问题):
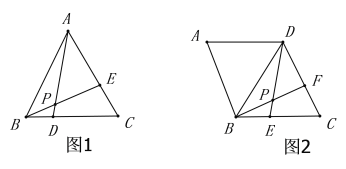
先出示问题(1):如图1,在等边三角形![]() 中,
中,![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 上一点,如果
上一点,如果![]() ,连接
,连接![]() 、
、![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,求
,求![]() 的度数.
的度数.
通过学习,王老师请同学们说说自己的收获.小明说发现一个结论:在这个等边三角形![]() 中,只要满足
中,只要满足![]() ,则
,则![]() 的度数就是一个定值,不会发生改变.紧接着王老师出示了问题(2):如图2,在菱形
的度数就是一个定值,不会发生改变.紧接着王老师出示了问题(2):如图2,在菱形![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 上一点,
上一点,![]() ,连接
,连接![]() 、
、![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,如果
,如果![]() ,
,![]() ,求出菱形的边长.
,求出菱形的边长.
问题(3):通过以上的学习请写出你得到的启示(一条即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠A=90°,BD=BC,CE⊥BD于E.
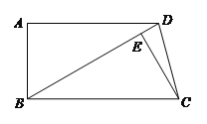
(1)求证:BE=AD;(2)若∠DCE=15°,AB=2,求在四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小刚和小红打算各自随机选择本周日的上午或下午去扬州马可波罗花世界游玩.
![]() 小明和小刚都在本周日上午去游玩的概率为________;
小明和小刚都在本周日上午去游玩的概率为________;
![]() 求他们三人在同一个半天去游玩的概率.
求他们三人在同一个半天去游玩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,角α的两边与双曲线y=![]() (k<0,x<0)交于A、B两点,在OB上取点C,作CD⊥y轴于点D,分别交双曲线y=
(k<0,x<0)交于A、B两点,在OB上取点C,作CD⊥y轴于点D,分别交双曲线y=![]() 、射线OA于点E、F,若OA=2AF,OC=2CB,则
、射线OA于点E、F,若OA=2AF,OC=2CB,则![]() 的值为______.
的值为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com