
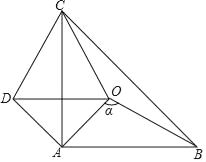
【题目】如图,△ABC和△AOD是等腰直角三角形,AB=AC,AO=AD,∠BAC=∠OAD=90°,点O是△ABC内的一点,∠BOC=130°.
(1)求证:OB=DC;
(2)求∠DCO的大小;
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.
【答案】(1)证明见解析;(2)40°;(3)当α的度数为115°或85°或145°时,△AOD是等腰三角形.
【解析】
(1)由已知证明△AOB≌△ADC,根据全等三角形的性质即可证得;
(2)由∠BOC=130°,根据周角的定义可得∠BOA+∠AOC=230°,再根据全等三角形的性质继而可得∠ADC+∠AOC=230°,由∠DAO=90°,在四边形AOCD中,根据四边形的内角和即可求得∠DCO的度数;
(3)分三种情况进行讨论即可得.
(1)∵∠BAC=∠OAD=90°,
∴∠BAC﹣∠CAO=∠OAD﹣∠CAO,
∴∠DAC=∠OAB,
在△AOB与△ADC中,
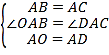 ,
,
∴△AOB≌△ADC,
∴OB=DC;
(2)∵∠BOC=130°,
∴∠BOA+∠AOC=360°﹣130°=230°,
∵△AOB≌△ADC
∠AOB=∠ADC,
∴∠ADC+∠AOC=230°,
又∵△AOD是等腰直角三角形,
∴∠DAO=90°,
∴四边形AOCD中,∠DCO=360°﹣90°﹣230°=40°;
(3)当CD=CO时,
∴∠CDO=∠COD=![]() =70°,
=70°,
∵△AOD是等腰直角三角形,
∴∠ODA=45°,
∴∠CDA=∠CDO+∠ODA=70°+45°=115°,
又∠AOB=∠ADC=α,
∴α=115°;
当OD=CO时,
∴∠DCO=∠CDO=40°,
∴∠CDA=∠CDO+∠ODA=40°+45°=85°,
∴α=85°;
当CD=OD时,
∴∠DCO=∠DOC=40°,
∠CDO=180°﹣∠DCO﹣∠DOC=180°﹣40°﹣40°=100°,
∴∠CDA=∠CDO+∠ODA=100°+45°=145°,
∴α=145°,
综上所述:当α的度数为115°或85°或145°时,△AOD是等腰三角形.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是 ( )
A. ∠A=∠C-∠B B. a2=b2-c2 C. a:b:c=2:3:4 D. a=![]() ,b=
,b=![]() ,c=1
,c=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC, AD是∠BAC的平分线,DE⊥AB于E,DF ⊥AC于F,则下列说法:①DA平分∠EDF;②AE=AF,DE=DF;③AD上任意一点到B、C两点的距离相等;④图中共有3对全等三角形,其中正确的有
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,O为坐标原点,正方形OABC的定点A,B都在反比例函数y=![]() (k>0,x>0)的图象上,边BC与x轴交于点D,则
(k>0,x>0)的图象上,边BC与x轴交于点D,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
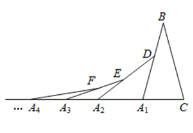
【题目】如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D,在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是______。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=1,则△A8B8A9的边长_________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB; ②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B间距离的有【 】

A.1组 B.2组 C.3组 D.4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,AB=BC,∠ABC=90°,F 为 AB 延长线上一点,点 E 在BC 上,且 AE=CF.

(1)求证: AE⊥CF;
(2)若∠CAE=25°,求∠ACF 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为 20 元/千克,售价不低于 20 元/千克,且不超过 32 元/千克,根据销售情况,发现该水果一天的销售量 y(千克)与该天的售价 x(元/千克)满足如下表所示的一次函数关系.
销售量 y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价 x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为 23.5 元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利 150 元,那么该天水果的售价为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com