
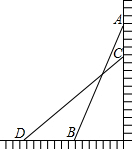
 如图,一架长25米的梯子,斜靠在竖直的墙上,这时梯子底端离墙7米.
如图,一架长25米的梯子,斜靠在竖直的墙上,这时梯子底端离墙7米.分析 (1)利用勾股定理可以得出梯子的顶端距离地面的高度.
(2)由(1)可以得出梯子的初始高度,下滑4米后,可得出梯子的顶端距离地面的高度,再次使用勾股定理,已知梯子的底端距离墙的距离为7米,可以得出,梯子底端水平方向上滑行的距离.
解答  解:(1)∵AB=25米,BE=7米,
解:(1)∵AB=25米,BE=7米,
梯子距离地面的高度AE=$\sqrt{2{5}^{2}-{7}^{2}}$=24米.
答:此时梯子顶端离地面24米;
(2)∵梯子下滑了4米,即梯子距离地面的高度CE=(24-4)=20米,
∴BD+BE=DE=$\sqrt{C{D}^{2}-C{E}^{2}}$=$\sqrt{2{5}^{2}-2{0}^{2}}$=15,
∴DE=15-7=8(米),即下端滑行了8米.
答:梯子底端将向左滑动了8米.
点评 本题考查的是勾股定理的应用,熟知勾股定理是解答此题的关键.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
 平面直角坐标系xOy中,抛物线y=mx2-2m2x+2交y轴于A点,交直线x=4于B点.
平面直角坐标系xOy中,抛物线y=mx2-2m2x+2交y轴于A点,交直线x=4于B点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 选取该校50名女生 | B. | 选取该校50名男生 | ||
| C. | 选取该校一个班级的学生 | D. | 随机选取该校50名学生 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-(x-2)2-1 | B. | y=(x+2)2-1 | C. | y=3(x-2)2+1 | D. | y=2(x-1)2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-1)2-3 | B. | (x-1)2+1 | C. | (x+1)2+2 | D. | (x+1)2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
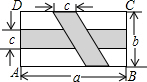 如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形,依照图中标注的数据,计算图中空白部分的面积,其面积是( )
如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形,依照图中标注的数据,计算图中空白部分的面积,其面积是( )| A. | bc-ab+ac+c2 | B. | a2+ab+bc-ac | C. | ab-bc-ac+c2 | D. | bc-ab+ac+c2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com