
【题目】一个多项式加上﹣3-x﹣2x2得到x2+1,这个多项式是________
科目:初中数学 来源: 题型:
【题目】(2016山西省第23题)综合与探究
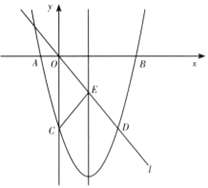
如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
(1)求抛物线的函数表达式,并分别求出点B和点E的坐标;
(2)试探究抛物线上是否存在点F,使![]() ≌
≌![]() ,若存在,请直接写出点F的坐标;若不存在,请说明理由;
,若存在,请直接写出点F的坐标;若不存在,请说明理由;
(3)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q.试探究:当m为何值时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某码头上有20名工人装载一批货物,已知每人往一艘轮船上装载2吨货物,装载完毕恰好用了6天,轮船到达目的地后,另一批工人开始卸货,计划平均每天卸货v吨,刚要卸货时遇到紧急情况,要求船上的货物卸载完毕不超过4天,则这批工人实际每天至少应卸货( )
A.30吨
B.40吨
C.50吨
D.60吨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪灵感.他惊喜地发现:当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连接DB,过点D作BC边上的高DF,则DF=EC=b-a.
∵S四边形ADCB=S△ACD+S△ABC=![]() b2+
b2+![]() ab.
ab.
又∵S四边形ADCB=S△ADB+S△DCB=![]() c2+
c2+![]() a(b-a),
a(b-a),
∴![]() b2+
b2+![]() ab=
ab=![]() c2+
c2+![]() a(b-a),
a(b-a),
∴a2+b2=c2.
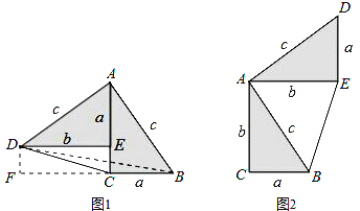
请参照上述证法,利用图2完成下面的证明:
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.
求证:a2+b2=c2.
证明:连接 ,
∵S五边形ACBED= ,
又∵S五边形ACBED= ,
∴ ,
∴a2+b2=c2.
查看答案和解析>>
科目:初中数学 来源: 题型:
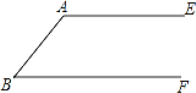
【题目】如图,AE∥BF,先按(1)的要求作图,再按(2)的要求证明
(1)用直尺和圆规作出∠ABF的平分线BD交AE于点D,再作出BD的中点O(不写作法,保留作图痕迹)
(2)连接(1)所作图中的AO并延长与BF相交于点C,连接DC,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为节约用水,某市居民生活用水按级收费,具体收费标准如下表:
用水量(吨) | 不超过15吨的部分 | 超过15不超过25吨的部分 | 超过25吨的部分 |
单位(元/吨) | 3 | 5 | 7 |
设李红家某月的为x吨(15<x25),应付水费为y元,则y关于x的函数表达式为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com