
”¾ĢāÄæ”æČēĶ¼1£¬ĖıߊĪABCDŗĶAEFGŹĒĮ½øö»„ĻąÖŲŗĻµÄ¾ŲŠĪ£¬ČēĶ¼2½«¾ŲŠĪAEFGČʵćA°“Ė³Ź±Õė·½ĻņŠż×Ŗ¦Į¶Č£Ø0”ܦĮ”Ü90”ć£©£¬µćGĒ”ŗĆĀäŌŚ¾ŲŠĪABCDµÄ¶Ō½ĒĻßÉĻ£¬ABÓėFGĻą½»ÓŚµćM£¬Į¬½ÓBE½»FGÓŚµćN£®
£Ø1£©µ±AB=ADŹ±£¬ĒėÖ±½ÓŠ“³ö”ĻABEµÄ¶ČŹż£»
£Ø2£©µ±”ĻADB=60”揱£¬Ēó”ĻABEµÄ¶ČŹż£»
£Ø3£©ČēĶ¼3£¬µ±AB=2AD=2Ź±£¬¢ŁĒóµćAµ½Ö±ĻßBEµÄ¾ąĄė£» ¢ŚÖ±½ÓŠ“³ö”÷BMNµÄÖܳ¤£®

”¾“š°ø”æ£Ø1£©”ĻABE=45”ć£»£Ø2£©”ĻABE=60”ć£»£Ø3£©µćAµ½Ö±ĻßBEµÄ¾ąĄėĪŖ![]() £»”÷BMNµÄÖܳ¤ĪŖ=
£»”÷BMNµÄÖܳ¤ĪŖ=![]() +
+![]() £®
£®
”¾½āĪö”æ
(1)µ±AB=ADŹ±,ÅŠ¶Ļ³öµćGŗĶµćBÖŲŗĻ,¼“æÉµĆ³ö½įĀŪ;
(2) ĻČÅŠ¶Ļ³ö”÷ADGŹĒµČ±ßČż½ĒŠĪ, µĆ³ö”ĻDAG=![]() , ŌŁÅŠ¶Ļ³ö”÷ABEŹĒµČ±ßČż½ĒŠĪ, ¼“æÉµĆ³ö½įĀŪ;
, ŌŁÅŠ¶Ļ³ö”÷ABEŹĒµČ±ßČż½ĒŠĪ, ¼“æÉµĆ³ö½įĀŪ;
(3)¢ŁĻČČ·¶Ø³öBD=![]() , sin”ĻADB=
, sin”ĻADB=![]() =
=![]() =COS”ĻABD, ½ų¶ųµĆ³öAQ=
=COS”ĻABD, ½ų¶ųµĆ³öAQ=![]() , ŌŁÅŠ¶Ļ³ö¦¤ADQ”צ¤ABH, ¼“æÉµĆ³ö½įĀŪ;
, ŌŁÅŠ¶Ļ³ö¦¤ADQ”צ¤ABH, ¼“æÉµĆ³ö½įĀŪ;
¢ŚĻČĒó³öBH=![]() , ¼“: BE=2BH=
, ¼“: BE=2BH=![]() ŌŁÅŠ¶Ļ³ö”ĻFEN=”ĻABD, ¼“æÉĒó³ö”ĻBNM, ×īŗóÓɦ¤BMN”צ¤BAE, Ēó³öM N=BM=
ŌŁÅŠ¶Ļ³ö”ĻFEN=”ĻABD, ¼“æÉĒó³ö”ĻBNM, ×īŗóÓɦ¤BMN”צ¤BAE, Ēó³öM N=BM=![]() , ¼“æÉµĆ³ö½įĀŪ.
, ¼“æÉµĆ³ö½įĀŪ.
½ā£ŗ£Ø1£©ČēĶ¼1£¬
µ±AB=ADŹ±£¬¾ŲŠĪABCDŗĶ¾ŲŠĪAEFG¶¼ŹĒÕż·½ŠĪ£¬
”ąŠż×ŖŹ¹µćGŌŚÕż·½ŠĪ¶Ō½ĒĻßÉĻŹ±£¬µćGŗĶµćBÖŲŗĻ£¬
ŌŚ”÷ABEÖŠ£¬”ĻBAE=90”ć£¬AE=AB£¬
”ą”ĻABE=45”ć£»
£Ø2£©ŌŚRt”÷ABDÖŠ£¬”ĻADB=60”ć£¬
ÓÉŠż×ŖÖŖ£¬AD=AG£¬
”ą”÷ADGŹĒµČ±ßČż½ĒŠĪ£¬
”ą”ĻDAG=60”ć£¬
”ą”ĻBAG=90”ć©60”ć=30”ć£¬
”ą”ĻBAE=90”ć©30”ć=60”ć£¬
”ßAB=AE£¬
”ą”÷ABEŹĒµČ±ßČż½ĒŠĪ£¬
”ą”ĻABE=60”ć£»
£Ø3£©¢ŁČēĶ¼3£¬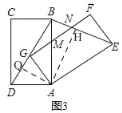
¹żµćA×÷AH”ĶBEÓŚH£¬
”ą”ĻBAH=![]() ”ĻBAE£¬
”ĻBAE£¬
”ąAH¾ĶŹĒµćAµ½Ö±ĻßBEµÄ¾ąĄė£¬
ŌŚRt”÷ABDÖŠ£¬AB=2AD=2£¬
”ąAD=1£¬øł¾Ż¹“¹É¶ØĄķµĆ£¬BD=![]() £¬sin”ĻADB=
£¬sin”ĻADB=![]() =
=![]() =
=![]() =cos”ĻABD£¬
=cos”ĻABD£¬
¹żµćA×÷AQ”ĶBDÓŚQ£¬
”ą”ĻDAQ=![]() ”ĻDAG£¬
”ĻDAG£¬
ŌŚRt”÷ADQÖŠ£¬tan”ĻADB=![]() =
=![]() £¬
£¬
”ąAQ=![]() AD=
AD=![]() £¬
£¬
ÓÉŠż×ŖÖŖ£¬”ĻDAG=”ĻBAE£¬
”ą”ĻDAQ=”ĻBAH£¬
”ß”ĻAQD=”ĻAHB£¬
”ą”÷ADQ”×”÷ABH£¬
”ą![]() =
=![]() £¬
£¬
”ąAH=![]() £¬
£¬
¼“£ŗµćAµ½Ö±ĻßBEµÄ¾ąĄėĪŖ![]() £»
£»
¢ŚÓÉ¢ŁÖŖ£¬AH=![]() £¬
£¬
ŌŚRt”÷ABHÖŠ£¬øł¾Ż¹“¹É¶ØĄķµĆ£¬BH=![]() =
=![]() £¬
£¬
”ąBE=2BH=![]() £¬
£¬
ÓÉ¢ŁÖŖ£¬”ĻABE=”ĻADB£¬
”ą”ĻNBG=90”ć£¬
”ß”ĻNFE=90”ć£¬
”ą”ĻFEN=”ĻBGN£¬
”ß”ĻBGN+”ĻQAG=90”ć£¬
”ą”ĻFEN=”ĻGAQ=”ĻDAQ=”ĻABD£¬
ŌŚRt”÷EFNÖŠ£¬cos”ĻFEN=![]() =cos”ĻABD=
=cos”ĻABD=![]() £¬
£¬
”ą![]() =
=![]() £¬
£¬
”ąEN=![]() £¬
£¬
”ąBN=BE©NE=![]() £¬
£¬
”ßMN”ĪAE£¬
”ą”÷BMN”×”÷BAE£¬
”ą![]() £¬
£¬
”ą=![]()
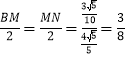 £¬
£¬
”ąMN=BM=![]() £¬
£¬
”ą”÷BMNµÄÖܳ¤ĪŖMN+BM+BN=![]() £®
£®


 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øö¶ž“ĪŗÆŹżĶ¼ĻóÉĻ²æ·ÖµćµÄŗį×ų±źx£¬×Ż×ų±źyµÄ¶ŌÓ¦ÖµČēĻĀ±ķ£ŗ
x | ” | ©4 | ©3 | ©2 | ©1 | 0 | 1 | 2 | 3 | 4 | ” |
y | ” | © | 0 |
| 2 |
| 0 | m | ©6 | © | ” |
£Ø1£©ĒóÕāøö¶ž“ĪŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©ĒómµÄÖµ£»
£Ø3£©ŌŚøų¶ØµÄÖ±½Ē×ų±źĻµÖŠ£¬»³öÕāøöŗÆŹżµÄĶ¼Ļó£»
£Ø4£©øł¾ŻĶ¼Ļ󣬊“³öµ±y£¼0Ź±£¬xµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
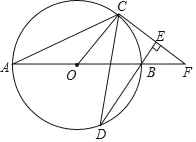
”¾ĢāÄæ”æČēĶ¼£¬ABĪŖ”ŃOÖ±¾¶£¬C”¢DĪŖ”ŃOÉĻ²»Ķ¬ÓŚA”¢BµÄĮ½µć£¬OCĘ½·Ö”ĻACD£¬¹żµćC×÷CE”ĶDB£¬“¹×ćĪŖE£¬Ö±ĻßABÓėÖ±ĻßCEĻą½»ÓŚFµć£®
£Ø1£©ĒóÖ¤£ŗCFĪŖ”ŃOµÄĒŠĻߣ»
£Ø2£©µ±BF=2£¬”ĻF=30”揱£¬ĒóBDµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
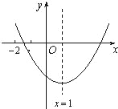
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹży=ax2+bx+c£Øa”Ł0£©µÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬ÓŠĻĀĮŠ½įĀŪ£ŗ
¢Łb2©4ac£¾0£»¢Śabc£¾0£»¢Ū8a+c£¾0£»¢Ü9a+3b+c£¼0£® ĘäÖŠ£¬ÕżČ·½įĀŪµÄÓŠ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
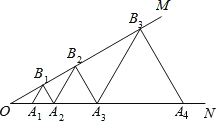
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ![]() £¬µć
£¬µć![]() £®£®£®ŌŚÉäĻß
£®£®£®ŌŚÉäĻß![]() ÉĻ£¬µć
ÉĻ£¬µć![]() £®£®£®ŌŚÉäĻß
£®£®£®ŌŚÉäĻß![]() ÉĻ£»
ÉĻ£»![]() £®£®£®¾łĪŖµČ±ßČż½ĒŠĪ£¬Čō
£®£®£®¾łĪŖµČ±ßČż½ĒŠĪ£¬Čō![]() £¬Ōņ
£¬Ōņ![]() µÄ±ß³¤ĪŖ£Ø£©
µÄ±ß³¤ĪŖ£Ø£©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠÅŠ¶ĻÕżČ·µÄŹĒ£Ø £©
A. ”°ČĪŅāŃ”ŌńijŅ»µēŹÓʵµĄ£¬ĖüÕżŌŚ²„·Å¶Æ»Ę¬”±ŹĒ±ŲČ»ŹĀ¼ž
B. ijŌĖ¶ÆŌ±Ķ¶Ņ»“ĪĄŗ£¬Ķ¶ÖŠµÄøÅĀŹĪŖ0.8£¬ŌņøĆŌĖ¶ÆŌ±Ķ¶5“ĪĄŗ£¬Ņ»¶ØÓŠ4“ĪĶ¶ÖŠ
C. ČĪŅāÅ×ÖĄŅ»Ć¶¾łŌȵÄÓ²±Ņ£¬·“Ćę³ÆÉĻµÄøÅĀŹĪŖ![]()
D. ²¼“üĄļÓŠ3øö°×Ēņ£¬1øöŗŚĒņ£®ČĪŅāČ”³ö1øöĒņ£¬Ē”ŗĆŹĒŗŚĒņµÄøÅĀŹŹĒ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”ŃCµÄ°ė¾¶ĪŖ2£¬Ō²ĶāŅ»µćOĀś×ćOC£½3.5£¬µćPĪŖ”ŃCÉĻŅ»¶Æµć£¬¾¹żµćOµÄÖ±ĻßlÉĻÓŠĮ½µćA”¢B£¬ĒŅOA£½OB£¬”ĻAPB£½90”ć£¬l²»¾¹żµćC£¬ŌņABµÄ×īŠ”ÖµĪŖ£Ø £©
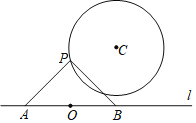
A. 2 B. 2.5 C. 3 D. 3.5
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
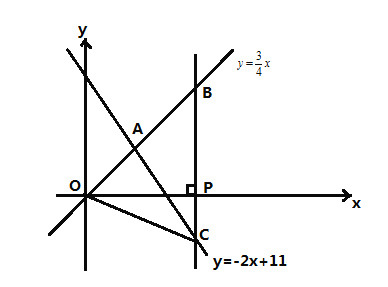
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ£¬ŅŃÖŖÕż±ČĄżŗÆŹż
ÖŠ£¬ŅŃÖŖÕż±ČĄżŗÆŹż![]() ÓėŅ»“ĪŗÆŹż
ÓėŅ»“ĪŗÆŹż![]() µÄĶ¼Ļó½»ÓŚµć
µÄĶ¼Ļó½»ÓŚµć![]() £¬Éč
£¬Éč![]() ÖįÉĻÓŠŅ»µć
ÖįÉĻÓŠŅ»µć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÖįµÄ“¹Ļߣؓ¹ĻßĪ»ÓŚµć
ÖįµÄ“¹Ļߣؓ¹ĻßĪ»ÓŚµć![]() µÄÓŅ²ą£©·Ö±š½»
µÄÓŅ²ą£©·Ö±š½»![]() ŗĶ
ŗĶ![]() µÄĶ¼ĻóÓėµć
µÄĶ¼ĻóÓėµć![]() ”¢
”¢![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬Čō
£¬Čō![]() £¬Ōņ
£¬Ōņ![]() µÄĆ껿ĪŖ£Ø £©
µÄĆ껿ĪŖ£Ø £©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
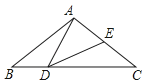
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬µćDŹĒ±ßBCÉĻµÄŅ»µć£¬µćEŹĒ±ßACÉĻµÄŅ»µć£¬ĒŅAB£½AC£½DC£¬BD£½CE£¬Į¬½ÓAD”¢DE£®
£Ø1£©ĒóÖ¤£ŗ”÷ADEŹĒµČŃüČż½ĒŠĪ£»
£Ø2£©Čō”ĻADE£½40”ć£¬ĒėĒó³ö”ĻBACµÄ¶ČŹż£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com