
【题目】下图是某汽车行驶的路程![]()
![]() 与时间
与时间![]() (分钟)的函数关系图.
(分钟)的函数关系图.
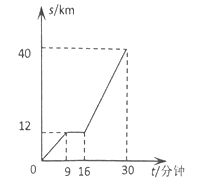
观察图中所提供的信息,解答下列问题:
(1)汽车在前![]() 分钟内的平均速度是 .
分钟内的平均速度是 .
(2)汽车在中途停了多长时间?
(3)当![]() 时,求
时,求![]() 与
与![]() 的函数关系式
的函数关系式
科目:初中数学 来源: 题型:
【题目】营市公交公司将淘汰所有线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
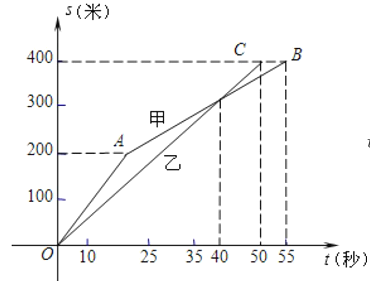
【题目】如图,在甲、乙两名同学进行400米跑步比赛中,路程S(米)与时间(t)之间的函数关系的图像分别为折线OAB和线段OC请根据图上信息回答下列问题
(1) 先到达终点;
(2)第 秒时, 追上 ;
(3)比赛过程中, 的速度适中保持不变;
(4)优胜者在比赛过程中所跑的路程S(米)关于时间t(秒)的函数解析式及定义域为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
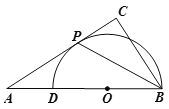
【题目】如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AC相切于点P.
(1)求证:BP平分∠ABC;
(2)若PC=1,AP=3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠α﹣∠β).正确的有( )
(∠α﹣∠β).正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,描述了林老师某日傍晚的一段生活过程:他晚饭后,从家里散步走到超市,在超市停留了一会儿,马上又去书店,看了一会儿书,然后快步走回家,图象中的平面直角坐标系中x表示时间,y表示林老师离家的距离,请你认真研读这个图象,根据图象提供的信息,以下说法错误的是( )

A. 林老师家距超市1.5千米
B. 林老师在书店停留了30分钟
C. 林老师从家里到超市的平均速度与从超市到书店的平均速度是相等的
D. 林老师从书店到家的平均速度是10千米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
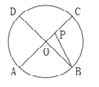
【题目】如图,A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿OC→![]() →DO的路线做匀速运动,当点P运动到圆心O时立即停止.设运动时间为
→DO的路线做匀速运动,当点P运动到圆心O时立即停止.设运动时间为![]() (s),∠APB的度数为y度,则下列图象中表示y(度)与 t(s)之间的函数关系最恰当的是 ( )
(s),∠APB的度数为y度,则下列图象中表示y(度)与 t(s)之间的函数关系最恰当的是 ( )
A. 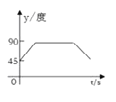 B.
B. 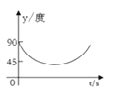 C.
C. 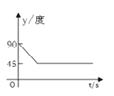 D.
D. 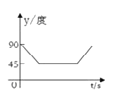
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明遇到这样一个问题:已知:在△ABC中,AB,BC,AC三边的长分别为![]() 、
、![]() 、
、![]() ,求△ABC的面积.
,求△ABC的面积.
小明是这样解决问题的:如图1所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积他把这种解决问题的方法称为构图法.
请回答:

(1)①图1中△ABC的面积为________;
②图1中过O点画一条线段MN,使MN=2AB,且M、N在格点上.
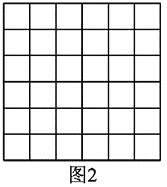
(2)图2是一个6×6的正方形网格(每个小正方形的边长为1).利用构图法在图2中画出三边长分别为![]() 、2
、2![]() 、
、![]() 的格点△DEF.
的格点△DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,E为正方形ABCD的边BC上一点,F为边BA延长线上一点,且CE=AF.

(1)求证:DE⊥DF;
(2)如图2,若点G为边AB上一点,且∠BGE=2∠BFE,△BGE的周长为16,求四边形DEBF的面积;
(3)如图3,在(2)的条件下,DG与EF交于点H,连接CH且CH=5![]() ,求AG的长.
,求AG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com