
 已知?ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC、PF⊥BD,垂足分别为E、F,PE=PF=$\sqrt{3}$,EO=1,AE=3,DF=5,S?ABCD=20$\sqrt{3}$.
已知?ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC、PF⊥BD,垂足分别为E、F,PE=PF=$\sqrt{3}$,EO=1,AE=3,DF=5,S?ABCD=20$\sqrt{3}$. 分析 连接OP,由HL证得Rt△OPE≌Rt△OPF,得出OE=OF=1,求出OA、OD的长,计算出S△APO、S△OPD,从而得出S△AOD,即可得出结果.
解答 解:连接OP,如图所示: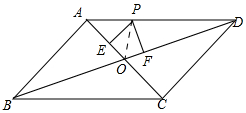
∵PE⊥AC、PF⊥BD,
∴在Rt△OPE和Rt△OPF中,$\left\{\begin{array}{l}{PE=PF}\\{OP=OP}\end{array}\right.$,
∴Rt△OPE≌Rt△OPF(HL),
∴OE=OF=1,
∴OA=AE+OE=3+1=4,OD=DF+OF=5+1=6,
S△APO=$\frac{1}{2}$PE•OA=$\frac{1}{2}$×$\sqrt{3}$×4=2$\sqrt{3}$,
S△OPD=$\frac{1}{2}$PF•OD=$\frac{1}{2}$×$\sqrt{3}$×6=3$\sqrt{3}$,
∴S△AOD=S△APO+S△OPD=2$\sqrt{3}$+3$\sqrt{3}$=5$\sqrt{3}$,
∵四边形ABCD为平行四边形,
∴S?ABCD=4×S△AOD=4×5$\sqrt{3}$=20$\sqrt{3}$,
故答案为20$\sqrt{3}$.
点评 本题主要考查了全等直角三角形的判定与性质、三角形面积的计算、平行四边形的性质等知识,熟练掌握全等直角三角形的判定与性质与平行四边形的性质是解决问题的关键.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:解答题
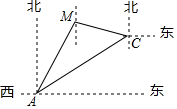 一渔船在海岛A北偏东30°方向的M处遇险,渔船将险情报告给位于A处的救援船后,沿南偏东75°方向向海岛C靠近,同时,从A处出发的救援船沿北偏东60°方向以每小时40$\sqrt{2}$海里的速度匀速航行,30分钟后,救援船在海岛C处恰好追上渔船,那么渔船遇险M处与海岛C的距离是多少海里?($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
一渔船在海岛A北偏东30°方向的M处遇险,渔船将险情报告给位于A处的救援船后,沿南偏东75°方向向海岛C靠近,同时,从A处出发的救援船沿北偏东60°方向以每小时40$\sqrt{2}$海里的速度匀速航行,30分钟后,救援船在海岛C处恰好追上渔船,那么渔船遇险M处与海岛C的距离是多少海里?($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a6÷a3=a2 | B. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{2}$ | C. | (-1)-1=1 | D. | (a3)2=a5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2000名考生是总体的一个样本 | |
| B. | 每个考生是个体 | |
| C. | 这5万名考生的数学中考成绩的全体是总体 | |
| D. | 统计中采用的调查方式是普查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
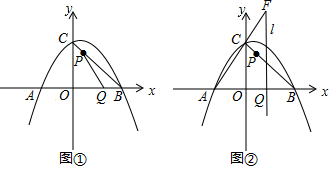
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
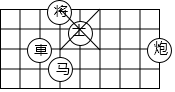 如图是棋盘的一部分,若用(1,3)表示
如图是棋盘的一部分,若用(1,3)表示 的位置,(2,2)表示
的位置,(2,2)表示 的位置,则
的位置,则 的位置可表示为( )
的位置可表示为( )| A. | (1,6) | B. | (6,1) | C. | (6,0) | D. | (7,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
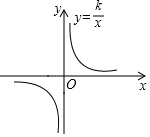 已知反比例函数y=$\frac{k}{x}$的图象如图所示,点A(1,y1),B(3,y2),C(-2,y3)都在该函数图象上,则y1,y2,y3的大小关系是( )
已知反比例函数y=$\frac{k}{x}$的图象如图所示,点A(1,y1),B(3,y2),C(-2,y3)都在该函数图象上,则y1,y2,y3的大小关系是( )| A. | y2<y3<y1 | B. | y3<y2<y1 | C. | y3<y2<y1 | D. | y2<y1<y3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com