
【题目】某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B两处出发,沿轨道到达C处,B在AC上,甲的速度是乙的速度的1.5倍,设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图,试根据图象解决下列问题:
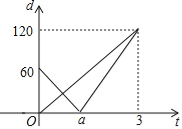
(1)填空:乙的速度v2= 米/分;
(2)写出d1与t的函数关系式:
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰?
【答案】(1)40;(2)d1=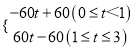 ;(3)0≤t<2.5.
;(3)0≤t<2.5.
【解析】试题分析:(1)根据路程与时间的关系,可得答案;
(2)根据甲的速度是乙的速度的1.5倍,可得甲的速度,根据路程与时间的关系,可得a的值,根据待定系数法,可得答案;
(3)根据两车的距离,可得不等式,根据解不等式,可得答案.
试题解析:(1)乙的速度v2=120÷3=40(米/分),
(2)v1=1.5v2=1.5×40=60(米/分),
60÷60=1(分钟),a=1,
d1=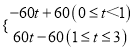 ;
;
(3)d2=40t,
当0≤t<1时,d2+d1>10,
即-60t+60+40t>10,
解得0≤t<2.5,
∵0≤t<1,
∴当0≤t<1时,两遥控车的信号不会产生相互干扰;
当1≤t≤3时,d2-d1>10,
即40t-(60t-60)>10,
当1≤t<![]() 时,两遥控车的信号不会产生相互干扰
时,两遥控车的信号不会产生相互干扰
综上所述:当0≤t<2.5时,两遥控车的信号不会产生相互干扰.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙0经过点D,E是⊙O上一点,且∠AED=45°,

(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为3,AE=5,求∠DAE的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD⊥DF,EC⊥DF,∠1=∠3,∠2=∠4,求证:AE∥DF.(请在下面的解答过程的空格内填空或在括号内填写理由)
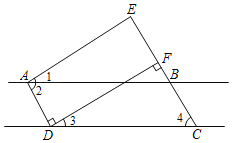
证明:∵AD⊥DF,EC⊥DF,(已知)
∴∠BFD=∠ADF=90°.( )
∴EC∥( )
∴∠EBA=_____(两直线平行,内错角相等)
∵∠2=∠4,(已知)
∴∠EBA=∠4.(等量代换)
∴AB∥_____.( )
∴∠2+∠ADC=180°.( )
∴∠2+∠ADF+∠3=180°.
∵∠1=∠3.(已知)
∴∠2+∠ADF+∠1=180°.(等量代换)
∴_____+∠ADF=180°.
∴AE∥DF.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P(-5,m)和Q(3,m)是二次函数y=2x2+bx+1图象上的两点.
(1)求b的值;
(2)将二次函数y=2x2+bx+1的图象沿y轴向上平移k(k>0)个单位,使平移后的图象与x轴无交点,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个机器人从数轴原点出发,沿数轴正方向,以每前进3步后退2步的程序运动。设该机器人每秒钟前进或后退1步,并且每步的距离是1个单位长,![]() 表示第
表示第![]() 秒时机器人在数轴上的位置所对应的数。给出下列结论:①
秒时机器人在数轴上的位置所对应的数。给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 。其中,正确的结论的序号是( )
。其中,正确的结论的序号是( )
A.①③B.②③C.①②③D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A点坐标为(5,0),直线y=kx+b(b>0)与y轴交于点B,∠BCA=60°,连接AB,∠α=105°,则直线y=kx+b的表达式为( )
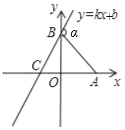
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题原型)如图,在![]() 中,对角线
中,对角线![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是菱形.
是菱形.
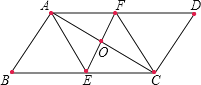
(小海的证法)证明:
![]()
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]()
![]() ,(第一步)
,(第一步)
![]() ,(第二步)
,(第二步)
![]() .(第三步)
.(第三步)
![]() 四边形
四边形![]() 是平行四边形.(第四步)
是平行四边形.(第四步)
![]() 四边形
四边形![]() 是菱形. (第五步)
是菱形. (第五步)
(老师评析)小海利用对角线互相平分证明了四边形![]() 是平行四边形,再利用对角线互相垂直证明它是菱形,可惜有一步错了.
是平行四边形,再利用对角线互相垂直证明它是菱形,可惜有一步错了.
(挑错改错)(1)小海的证明过程在第________步上开始出现了错误.
(2)请你根据小海的证题思路写出此题的正确解答过程,
查看答案和解析>>
科目:初中数学 来源: 题型:
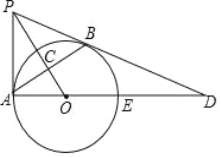
【题目】如图,PB与⊙O相切于点B,过点B作OP的垂线BA,垂足为C,交⊙O于点A,连结PA,AO,AO的延长线交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若tan∠BAD=![]() ,且OC=4,求BD的长.
,且OC=4,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com