



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题
 沿EF翻折,得到一个V字形图案。
沿EF翻折,得到一个V字形图案。
 ;(用尺规作图,不写画法,保留作图痕迹)
;(用尺规作图,不写画法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 +PB
+PB =PC
=PC ,证明∠PQC=90°;
,证明∠PQC=90°;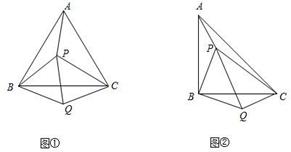
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=
度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF= ,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE.其中正确的是___________________(写出正确结论的序号)。
,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE.其中正确的是___________________(写出正确结论的序号)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com