
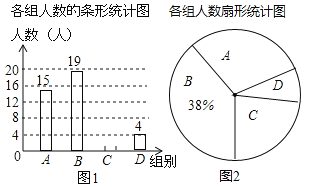
【题目】小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图(A:0<t≤10,B:10<t≤20,C:20<t≤30,D:t>30),根据图中信息,解答下列问题:
(1)这项被调查的总人数是多少人?
(2)试求表示A组的扇形统计图的圆心角的度数,补全条形统计图;
(3)如果小明想从D组的甲、乙、丙、丁四人中随机选择两人了解平时租用共享单车情况,请用列表或画树状图的方法求出恰好选中甲的概率.
 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
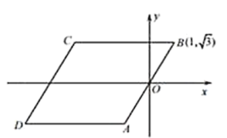
【题目】如图,已知四边形ABCD是菱形,BC∥x轴,点B的坐标是(1,![]() ),坐标原点O是AB的中点.动圆⊙P的半径是
),坐标原点O是AB的中点.动圆⊙P的半径是![]() ,圆心在x轴上移动,若⊙P在运动过程中只与菱形ABCD的一边相切,则点P的横坐标m 的取值范围是_________.
,圆心在x轴上移动,若⊙P在运动过程中只与菱形ABCD的一边相切,则点P的横坐标m 的取值范围是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
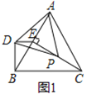
【题目】如图1,在等边![]() 和等边
和等边![]() 中,
中,![]() ,点P在
,点P在![]() 的高
的高![]() 上(点
上(点![]() 与点
与点![]() 不重合),点
不重合),点![]() 在点
在点![]() 的左侧,连接
的左侧,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
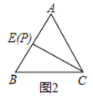
(2)当点![]() 与点
与点![]() 重合时,延长
重合时,延长![]() 交
交![]() 于点
于点![]() ,请你在图2中作出图形,并求出
,请你在图2中作出图形,并求出![]() 的长;
的长;
(3)直接写出线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
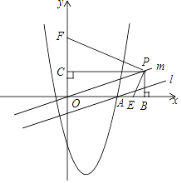
【题目】如图:在平面直角坐标系中,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,经过点
,经过点![]() 的抛物线
的抛物线![]() 的对称轴是
的对称轴是![]() .
.
(1)求抛物线的解析式.
(2)平移直线![]() 经过原点
经过原点![]() ,得到直线
,得到直线![]() ,点
,点![]() 是直线
是直线![]() 上任意一点,
上任意一点,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,若点
,若点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() ,
,![]() ,且
,且![]() .求证:
.求证:![]() .
.
(3)若(2)中的点![]() 坐标为
坐标为![]() ,点
,点![]() 是
是![]() 轴上的点,点
轴上的点,点![]() 是
是![]() 轴上的点,当
轴上的点,当![]() 时,抛物线上是否存在点
时,抛物线上是否存在点![]() ,使四边形
,使四边形![]() 是矩形?若存在,请求出点
是矩形?若存在,请求出点![]() 的坐标,如果不存在,请说明理由.
的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
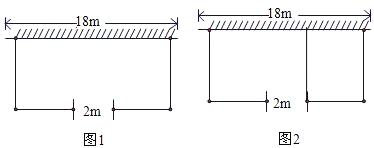
【题目】如图1,若要建一个长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米.
求:(1)若鸡场面积150平方米,鸡场的长和宽各为多少米?
(2)鸡场面积可能达到200平方米吗?
(3)如图2,若在鸡场内要用竹篱笆加建一道隔栏,则鸡场最大面积可达多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() (a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.
(a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.
(1)求抛物线的解析式;
(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点N从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,设△MBN的面积为S,点M运动时间为t,试求S与t的函数关系,并求S的最大值;
(3)在点M运动过程中,是否存在某一时刻t,使△MBN为直角三角形?若存在,求出t值;若不存在,请说明理由.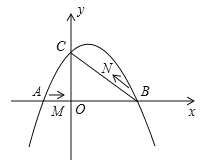
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“共和国勋章”是中华人民共和国的最高荣誉勋章,在2019年获得“共和国勋章”的八位杰出人物中,有于敏、孙家栋、袁隆平、黄旭华四位院士.如图是四位院士(依次记为![]() 、
、![]() 、
、![]() 、
、![]() ).为让同学们了解四位院士的贡献,老师设计如下活动:取四张完全相同的卡片,分别写上
).为让同学们了解四位院士的贡献,老师设计如下活动:取四张完全相同的卡片,分别写上![]() 、
、![]() 、
、![]() 、
、![]() 四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应院士的资料,并做成小报.
四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应院士的资料,并做成小报.
(1)班长在四种卡片中随机抽到标号为C的概率为______.
(2)请用画树状图或列表的方法求小明和小华查找不同院士资料的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是一张直角三角形纸片,其中
是一张直角三角形纸片,其中![]() ,
,![]() ,小亮将它绕点
,小亮将它绕点![]() 逆时针旋转后
逆时针旋转后![]() 得到
得到![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.

(1)如图1,当![]() 时,
时,![]() 所在直线与线段
所在直线与线段![]() 有怎样的位置关系?请说明理由.
有怎样的位置关系?请说明理由.
(2)如图2,当![]() ,求
,求![]() 为等腰三角形时的度数.
为等腰三角形时的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com