
【题目】已知在矩形AEFD中,点C为EF上一点,点B为FE的延长线上一点,连接CD、AB,![]() .
.
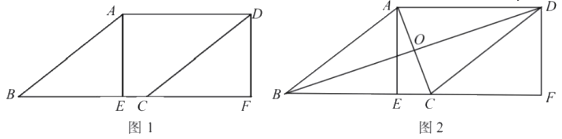
(1)如图1,求证:![]() ;
;
(2)如图2,连接BD、AC交于点![]() ,若
,若![]() ,在不添加任何辅助线的情况下,请直接写出图2中四个直角三角形,使写出的每个三角形的面积等于四边形
,在不添加任何辅助线的情况下,请直接写出图2中四个直角三角形,使写出的每个三角形的面积等于四边形![]() 的
的![]() .
.
【答案】(1)见解析;(2)![]() 、
、![]() 、
、![]() ,
,![]() .
.
【解析】
(1))根据矩形的性质得到![]() 和
和![]() ,再证明
,再证明![]() ,即可得到答案;
,即可得到答案;
(2)根据题目所给的条件,三角形的面积公式即可直接写出答案;
(1)证明:∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]()
∴∠![]()
∵![]() ,
,
∴![]() (HL),
(HL),
∴![]() ,
,
(2)由(1)知:![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵BC∥EF,
∴四边形ABCD是平行四边形,
∴AO=CO,BO=DO(平行四边形对角线相互平分),
又∵![]() ,
,
∴△ABO≌△ADO(SSS),
又∵AD=EF=BC(等量替换),
∴△AOD≌△COB(SSS),
又∵∠AOC= ∠COD(对顶角相等),
∴△ABO≌△CDO(SAS),
∴△ABO≌△ADO≌△CBO≌△CDO,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
故结果为:![]() 、
、![]() 、
、![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() ,B是边AD上一点,以AB为直径的
,B是边AD上一点,以AB为直径的![]() 经过点P,C是
经过点P,C是![]() 上一动点,连接AC,PC,PC交AB于点E,且
上一动点,连接AC,PC,PC交AB于点E,且![]() .
.
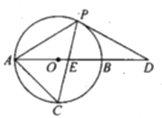
(1)求证:PD是![]() 的切线;
的切线;
(2)连接OP,PB,BC,OC,若![]() 的直径是4,则:
的直径是4,则:
①当四边形APBC是矩形时,求DE的长;
②当![]() ______时,四边形OPBC是菱形.
______时,四边形OPBC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴快车是一种便捷的出行工具,计价规则如下表:
计费项目 | 里程费 | 时长费 | 远途费 |
单价 | 1.8元/千米 | 0.3元/分 | 0.8元/千米 |
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为行车里程7千米以内(含7千米)不收远途费,超过7千米的,超出部分每千米收0.8元. | |||
(1)小王与小张各自乘坐滴滴快车,在同一地点约见,已知到达约见地点,他们的实际行车里程分别为6千米与8.5千米,两人付给滴滴快车的乘车费相同(1)求这两辆滴滴快车的实际行车时间相差多少分钟;
(2)实际乘车时间较少的人,由于出发时间比另一人早,所以提前到达约见地点在大厅等候.已知他等候另一人的时间是他自己实际乘车时间的1.5倍,且比另一人的实际乘车时间的一半多8.5分钟,计算两人各自的实际乘车时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() (
(![]() 在
在![]() 的左侧),交
的左侧),交![]() 轴于点
轴于点![]() ,且
,且![]() ,
,![]() .
.
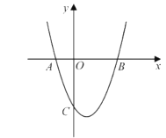
(1)求抛物线的解析式;
(2)点![]() 为第四象限抛物线上一点,过点
为第四象限抛物线上一点,过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,设
,设![]() 点横坐标为
点横坐标为![]() ,线段
,线段![]() 的长度为
的长度为![]() ,求
,求![]() 与
与![]() 的函数关系式.(不要求写出
的函数关系式.(不要求写出![]() 的取值范围)
的取值范围)
(3)在(2)的条件下,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() .
.
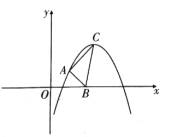
(1)求![]() ,
,![]() 的值;
的值;
(2)已知![]() 点为抛物线上异于
点为抛物线上异于![]() 的一点,且
的一点,且![]() 点横、纵坐标相等,
点横、纵坐标相等,![]() 为
为![]() 轴上任意一点,当
轴上任意一点,当![]() 取最小值时,求出
取最小值时,求出![]() 点坐标和此时
点坐标和此时![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门) .对调查结果进行整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

![]() 本次调查的学生共有___ 人,在扇形统计图中,
本次调查的学生共有___ 人,在扇形统计图中,![]() 的值是_ ;
的值是_ ;
![]() 将条形统计图补充完整;
将条形统计图补充完整;
![]() 在被调查的选修书法的学生中,有
在被调查的选修书法的学生中,有![]() 名为女同学,其余为男同学,现要从选修书法的同学中随机抽取
名为女同学,其余为男同学,现要从选修书法的同学中随机抽取![]() 名同学代表学校参加某社区组织的书法活动,请你用列表或画树状图的方法.求所抽取的
名同学代表学校参加某社区组织的书法活动,请你用列表或画树状图的方法.求所抽取的![]() 名同学恰好是
名同学恰好是![]() 名男同学和
名男同学和![]() 名女同学的概率.
名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,给定一个正方形,要通过画线将其分割成若干个互不重叠的正方形.第1次画线分割成4个互不重叠的正方形,得到图2;第2次画线分割成7个互不重叠的正方形,得到图3……以后每次只在上次得到图形的左上角的正方形中画线.
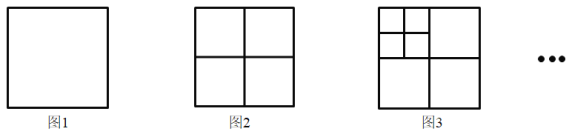
尝试:第3次画线后,分割成 个互不重叠的正方形;
第4次画线后,分割成 个互不重叠的正方形.
发现:第n次画线后,分割成 个互不重叠的正方形;并求第2020次画线后得到互不重叠的正方形的个数.
探究:若干次画线后,能否得到1001个互不重叠的正方形?若能,求出是第几次画线后得到的;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点p为边AB上的一点,![]() CPB=60°,沿CP折叠正方形后,点B落在平面内B’处,B’的坐标为( )
CPB=60°,沿CP折叠正方形后,点B落在平面内B’处,B’的坐标为( )
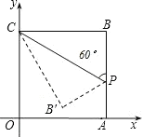
A.(2, 2![]() )B.(
)B.(![]() , 2-2
, 2-2![]() )C.(2, 4-2
)C.(2, 4-2![]() )D.(
)D.(![]() , 4-2
, 4-2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数![]() 的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )
的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com