
【题目】如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为 . 
【答案】1或 ![]()
【解析】解:分两种情况: ①如图1,过A′作MN∥CD交AD于M,交BC于N,
则直线MN是矩形ABCD 的对称轴,
∴AM=BN= ![]() AD=1,
AD=1,
∵△ABE沿BE折叠得到△A′BE,
∴A′E=AE,A′B=AB=1,
∴A′N= ![]() =0,即A′与N重合,
=0,即A′与N重合,
∴A′M=1,
∴A′E2=EM2+A′M2 ,
∴A′E2=(1﹣A′E)2+12 ,
解得:A′E=1,
∴AE=1;
②如图2,过A′作PQ∥AD交AB于P,交CD于Q,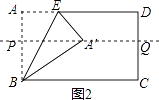
则直线PQ是矩形ABCD 的对称轴,
∴PQ⊥AB,AP=PB,AD∥PQ∥BC,
∴A′B=2PB,
∴∠PA′B=30°,
∴∠A′BC=30°,
∴∠EBA′=30°,∴AE=A′E=A′B×tan30°=1× ![]() =
= ![]() ;
;
综上所述:AE的长为1或 ![]() ;
;
故答案为:1或 ![]() .
.
分两种情况:①过A′作MN∥CD交AD于M,交BC于N,则直线MN是矩形ABCD 的对称轴,得出AM=BN= ![]() AD=1,由勾股定理得到A′N=0,求得A′M=1,再由勾股定理解得A′E即可;
AD=1,由勾股定理得到A′N=0,求得A′M=1,再由勾股定理解得A′E即可;
②过A′作PQ∥AD交AB于P,交CD于Q;求出∠EBA′=30°,由三角函数求出AE=A′E=A′B×tan30°;即可得出结果.


科目:初中数学 来源: 题型:
【题目】已知:AB是⊙O的弦,点C是 ![]() 的中点,连接OB、OC,OC交AB于点D.
的中点,连接OB、OC,OC交AB于点D.
(1)如图1,求证:AD=BD; 
(2)如图2,过点B作⊙O的切线交OC的延长线于点M,点P是 ![]() 上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°;
上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°; 
(3)如图3,在(2)的条件下,连接DP、MP,延长MP交⊙O于点Q,若MQ=6DP,sin∠ABO= ![]() ,求
,求 ![]() 的值.
的值. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上小芳,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 ![]() MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=8,AB=30,请你帮助她算一下△ABD的面积是( )
MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=8,AB=30,请你帮助她算一下△ABD的面积是( ) 
A.150
B.130
C.240
D.120
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某微店销售甲、乙两种商品,卖出6件甲商品和4件乙商品可获利120元;卖出10件甲商品和6件乙商品可获利190元.
(1)甲、乙两种商品每件可获利多少元?
(2)若该微店甲、乙两种商品预计再次进货200件,全部卖完后总获利不低于2300元,已知甲商品的数量不少于120件.请你帮忙设计一个进货方案,使总
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED= ![]() AB中,一定正确的是( )
AB中,一定正确的是( ) 
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3800米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“蒙上眼睛射击正中靶心”是必然事件
B.“抛一枚硬币,正面朝上的概率为 ![]() ”说明掷一枚质地均匀的硬币10次,必有5次正面朝上
”说明掷一枚质地均匀的硬币10次,必有5次正面朝上
C.“抛一枚均匀的正方体骰子,朝上的点数是3的概率为 ![]() ”表示随着抛掷次数的增加,“抛出朝上的点数是3”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数是3”这一事件发生的频率稳定在 ![]() 附近
附近
D.为了解某种节能灯的使用寿命,应选择全面调查
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com