
【题目】如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=![]() x相交于点A.
x相交于点A.
(1)求A点坐标;
(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,则P点坐标是 ;
(3)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.

【答案】(1)A点坐标是(2,3);(2)(0,![]() );(3)存在;点Q是坐标是(
);(3)存在;点Q是坐标是(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)联立方程,解方程即可求得;
(2)设P点坐标是(0,y),根据勾股定理列出方程,解方程即可求得;
(3)分两种情况:①当Q点在线段AB上:作QD⊥y轴于点D,则QD=x,根据S△OBQ=S△OAB-S△OAQ列出关于x的方程解方程求得即可;②当Q点在AC的延长线上时,作QD⊥x轴于点D,则QD=-y,根据S△OCQ=S△OAQ-S△OAC列出关于y的方程解方程求得即可.
(1)解方程组: 得:
得:![]()
∴A点坐标是(2,3);
(2)设P点坐标是(0,y),
∵△OAP是以OA为底边的等腰三角形,
∴OP=PA,
∴22+(3﹣y)2=y2,
解得y=![]() ,
,
∴P点坐标是(0,![]() ),
),
故答案为(0,![]() );
);
(3)存在;
由直线y=﹣2x+7可知B(0,7),C(![]() ,0),
,0),
∵S△AOC=![]() ×
×![]() ×3=
×3=![]() <6,S△AOB=
<6,S△AOB=![]() ×7×2=7>6,
×7×2=7>6,
∴Q点有两个位置:Q在线段AB上和AC的延长线上,设点Q的坐标是(x,y),
当Q点在线段AB上:作QD⊥y轴于点D,如图①,则QD=x,

∴S△OBQ=S△OAB﹣S△OAQ=7﹣6=1,
∴![]() OBQD=1,即
OBQD=1,即![]() ×7x=1,
×7x=1,
∴x=![]() ,
,
把x=![]() 代入y=﹣2x+7,得y=
代入y=﹣2x+7,得y=![]() ,
,
∴Q的坐标是(![]() ,
,![]() ),
),
当Q点在AC的延长线上时,作QD⊥x轴于点D,如图②则QD=﹣y,

∴S△OCQ=S△OAQ﹣S△OAC=6﹣![]() =
=![]() ,
,
∴![]() OCQD=
OCQD=![]() ,即
,即![]() ×
×![]() ×(﹣y)=
×(﹣y)=![]() ,
,
∴y=﹣![]() ,
,
把y=﹣![]() 代入y=﹣2x+7,解得x=
代入y=﹣2x+7,解得x=![]() ,
,
∴Q的坐标是(![]() ,﹣
,﹣![]() ),
),
综上所述:点Q是坐标是(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠C=90°,延长CA至点D,使AD=AB.设F为线段AB上一点,连接DF,以DF为斜边作等腰Rt△DEF,且使AE⊥AB.
(1)求证:AE=AF+BC;
(2)当点F为BA延长线上一点,而其余条件保持不变,如图2所示,试探究AE、AF、BC之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c>0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0; 其中正确的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
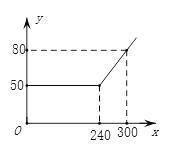
【题目】某网络公司推出了一系列上网包月业务,其中的一项业务是10M40元包240小时,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,小刚和小明家正好选择了这项上网业务.
(1)当x≥240时,求y与x之间的函数关系式;
(2)若小刚家10月份上网200小时,则他家应付多少元上网费?
(3)若小明家10月份上网费用为62元,则他家该月的上网时间是多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.

(1)概念理解:
如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)问题探究:
如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求![]() 的值.
的值.
(3)应用拓展:
如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的![]() 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,E,D是BC边的三等分点,F是AC的中点,BF分别交AD,AE于点G,H,则BG∶GH∶HF等于( )
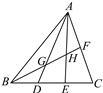
A. 1∶2∶3 B. 3∶5∶2 C. 5∶3∶2 D. 5∶3∶1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com