
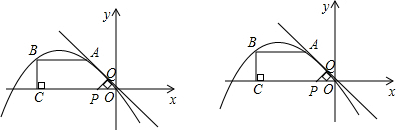
分析 (1)根据待定系数法,可得函数解析式;
(2)根据正方形对角顶点的横坐标的和相等,纵坐标的和相等,可得答案;
(3)①根据函数图象上点的坐标满足函数解析式,可得关于t的方程,根据解方程,可得答案;
②分类讨论:k=1时,根据三角形的面积公式,可得方程,根据解方程,可得答案;k=2时,根据相似三角形的性质,可得梯形的上底,根据梯形的面积公式,可得方程,根据解方程,可得答案.
解答 解:(1)将点A(-1,1),B(-3,1)代入函数解析式,得
$\left\{\begin{array}{l}{a-b=1}\\{9a-3b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=-\frac{4}{3}}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{3}$x2-$\frac{4}{3}$x;
(2)①P(-2t,0),Q在PO的垂直平分线上,Q,(-t,t),
设M(-a,a),
QM=PQ=$\sqrt{2}$t,
(-a+t)2+(a-t)2=2t2,
解得a=-2t,即M(-2t,2t);
PM的中点也是QN的中点,
N点的横坐标-2t+(-2t)-(-t)=-3t,N点的纵坐标2t-t=t,
N(-3t,t),
M(-2t,2t),N(-3t,t),
②当点M在抛物线上时,
2t=-$\frac{1}{3}$(-2t)2-$\frac{4}{3}$(-2t).
解得t=0(舍),t=$\frac{1}{2}$;
当点N在抛物线上时,
t=-$\frac{1}{3}$(-3t)2-$\frac{4}{3}$(-3t),
解得t=0(舍),或t=1,
∴t的值为$\frac{1}{2}$或1.
(3)由4k-3<k+6,得
k=1或k=2,
当k=1时,如图1: ,
,
S=$\frac{9}{16}{k}^{2}$=$\frac{9}{16}$=$\frac{1}{2}$($\sqrt{2}$t)2,
解得t=$\frac{3}{4}$,
当k=2时,S=$\frac{9}{16}{k}^{2}$=$\frac{9}{4}$,
如图2,Q2E⊥OP2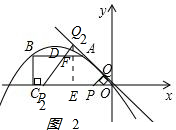 ,
,
OP2=2t,OE=Q2E=t,Q2F=t-1,
$\frac{FA}{OE}$=$\frac{{Q}_{2}F}{{Q}_{2}E}$,即FA=$\frac{(t-1)t}{t}$=t-1,
AD=2AF=2(t-1),
四边形OAFP2=$\frac{1}{2}$(2t-2+2t)×1=$\frac{9}{4}$,
解得t=$\frac{13}{8}$,
综上所述:$\frac{3}{4}$或$\frac{13}{8}$.
点评 本题考查了二次函数综合题,(1)利用了待定系数法求函数解析式,(2)利用正方形对角顶点的横坐标的和相等,纵坐标的和相等是解题关键;(3)利用了三角形的面积公式,梯形的面积公式得出方程是解题关键,要分类讨论,以防遗漏.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
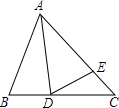 己知:如图,等边△ABC中,D、E分别是BC、AC上的点,且∠ADE=60°
己知:如图,等边△ABC中,D、E分别是BC、AC上的点,且∠ADE=60°查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
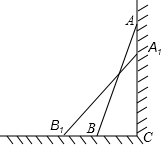 小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真地探索.思考题.如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真地探索.思考题.如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com