
【题目】如图,已知抛物线y=ax2+bx+4与x轴交于A(﹣2,0)、B两点,与y轴交于C点,其对称轴为直线x=1.
(1)直接写出抛物线的解析式:;
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形?若存在,求出E、F的坐标;若不存在,请说明理由.
【答案】
(1)y=﹣ ![]() x2+x+4
x2+x+4
(2)
解:由抛物线y=﹣ ![]() x2+x+4可知C(0,4),
x2+x+4可知C(0,4),
∵抛物线的对称轴为直线x=1,根据对称性,
∴C′(2,4),
∴A′(0,0)
(3)
解:存在.
设F(x,﹣ ![]() x2+x+4).
x2+x+4).
以A、C、E、F为顶点的四边形为平行四边形,
①若AC为平行四边形的边,如答图1﹣1所示,则EF∥AC且EF=AC.
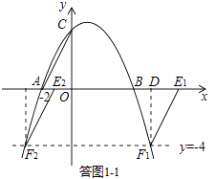
过点F1作F1D⊥x轴于点D,则易证Rt△AOC≌Rt△E1DF1,
∴DE1=2,DF1=4.
∴﹣ ![]() x2+x+4=﹣4,
x2+x+4=﹣4,
解得:x1=1+ ![]() ,x2=1﹣
,x2=1﹣ ![]() .
.
∴F1(1+ ![]() ,﹣4),F2(1﹣
,﹣4),F2(1﹣ ![]() ,﹣4);
,﹣4);
∴E1(3+ ![]() ,0),E2(3﹣
,0),E2(3﹣ ![]() ,0).
,0).
②若AC为平行四边形的对角线,如答图1﹣2所示.
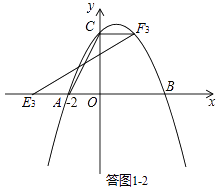
∵点E3在x轴上,∴CF3∥x轴,
∴点C为点A关于x=1的对称点,
∴F3(2,4),CF3=2.
∴AE3=2,
∴E3(﹣4,0),
综上所述,存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形;
点E、F的坐标为:E1(3+ ![]() ,0),F1(1+
,0),F1(1+ ![]() ,﹣4);E2(3﹣
,﹣4);E2(3﹣ ![]() ,0),F2(1﹣
,0),F2(1﹣ ![]() ,﹣4);E3(﹣4,0),F3(2,4)
,﹣4);E3(﹣4,0),F3(2,4)
【解析】解:(1)∵A(﹣2,0),对称轴为直线x=1.
∴B(4,0),
把A(﹣2,0),B(4,0)代入抛物线的表达式为:![]() ,
,
解得: 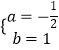 ,
,
∴抛物线的解析式为:y=﹣ ![]() x2+x+4;
x2+x+4;
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】二次函数图象的顶点在原点O,经过点A(1, ![]() );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.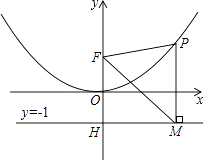
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(3,0),与y轴交于C(0,3),顶点为D(1,4),对称轴为DE.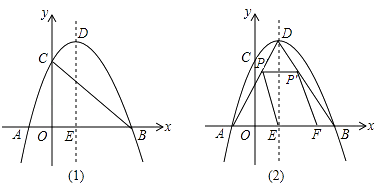
(1)抛物线的解析式是;
(2)如图(2),点P是AD上一个动点,P′是P关于DE的对称点,连接PE,过P′作P′F∥PE交x轴于F.设S四边形EPP′F=y,EF=x,求y关于x的函数关系式,并求y的最大值;
(3)在(1)中的抛物线上是否存在点Q,使△BCQ成为以BC为直角边的直角三角形?若存在,求出Q的坐标;若不存在.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初,小芳和小亮去学校商店购买学习用品,小芳用30元钱购买钢笔的数量是小亮用25元钱购买笔记本数量的2倍,已知每支钢笔的价格比每本笔记本的价格少2元
(1)求每支钢笔和每本笔记本各是多少元;
(2)学校运动会后,班主任再次购买上述价格的钢笔和笔记本共50件作为奖品,奖励给校运动会中表现突出的同学,总费用不超过200元.请问至少要买多少支钢笔?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进某种茶壶、茶杯共200个进行销售,其中茶杯的数量是茶壶数量的5倍还多20个.销售方式有两种:(1)单个销售;(2)成套销售.相关信息如下表:
进价(元/个) | 单个售价(元/个) | 成套售价(元/套) | |
茶壶 | 24 | a | 55 |
茶杯 | 4 | a﹣30 | |
备注:(1)一个茶壶和和四个茶杯配成一套(如图); (2)利润=(售价﹣进价)×数量 | |||
(1)该商店购进茶壶和茶杯各有多少个?
(2)已知甲顾客花180元购买的茶壶数量与乙顾客花30元购买的茶杯数量相同.
①求表中a的值.
②当该商店还剩下20个茶壶和100个茶杯时,商店将这些茶壶和茶杯中的一部分按成套销售,其余按单个销售,这120个茶壶和茶杯全部售出后所得的利润为365元.问成套销售了多少套?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G. 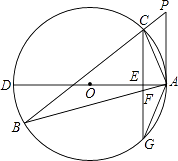
(1)判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AFAB;
(3)若⊙O的直径为10,AC=2 ![]() ,AB=4
,AB=4 ![]() ,求△AFG的面积.
,求△AFG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )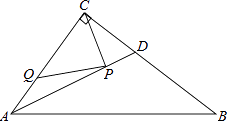
A.![]()
B.4
C.![]()
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在开展“美丽广西,清洁乡村”的活动中某乡镇计划购买A、B两种树苗共100棵,已知A种树苗每棵30元,B种树苗每棵90元.
(1)设购买A种树苗x棵,购买A、B两种树苗的总费用为y元,请你写出y与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)如果购买A、B两种树苗的总费用不超过7560元,且B种树苗的棵数不少于A种树苗棵数的3倍,那么有哪几种购买树苗的方案?
(3)从节约开支的角度考虑,你认为采用哪种方案更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈ ![]() ,tan48°≈
,tan48°≈ ![]() ,sin64°≈
,sin64°≈ ![]() ,tan64°≈2)
,tan64°≈2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com