
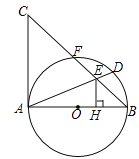
【题目】如图,已知AB为⊙O直径,AC是⊙O的切线,连接BC交⊙O于点F,取![]() 的中点D,连接AD交BC于点E,过点E作EH⊥AB于H.
的中点D,连接AD交BC于点E,过点E作EH⊥AB于H.
(1)求证:△HBE∽△ABC;
(2)若CF=4,BF=5,求AC和EH的长.
【答案】(1)证明见解析;(2)CA=6,EH=2.
【解析】(1)根据切线的性质即可证明:∠CAB=∠EHB,由此即可解决问题;
(2)连接AF.由△CAF∽△CBA,推出CA2=CFCB=36,推出CA=6,AB=![]() ,AF=
,AF=![]() ,由Rt△AEF≌Rt△AEH,推出AF=AH=2
,由Rt△AEF≌Rt△AEH,推出AF=AH=2![]() ,设EF=EH=x.在Rt△EHB中,可得(5﹣x)2=x2+(
,设EF=EH=x.在Rt△EHB中,可得(5﹣x)2=x2+(![]() )2,解方程即可解决问题;
)2,解方程即可解决问题;
(1)∵AC是⊙O的切线,
∴CA⊥AB.
∵EH⊥AB,
∴∠EHB=∠CAB.
∵∠EBH=∠CBA,
∴△HBE∽△ABC.
(2)连接AF.

∵AB是直径,
∴∠AFB=90°.
∵∠C=∠C,∠CAB=∠AFC,
∴△CAF∽△CBA,
∴CA2=CFCB=36,
∴CA=6,AB=![]() ,AF=
,AF=![]() .
.
∵![]() ,
,
∴∠EAF=∠EAH.
∵EF⊥AF,EH⊥AB,
∴EF=EH.
∵AE=AE,
∴Rt△AEF≌Rt△AEH,
∴AF=AH=2![]() .
.
设EF=EH=x.在Rt△EHB中,(5﹣x)2=x2+(![]() )2,
)2,
∴x=2,
∴EH=2.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】灌云教育局为了解今年九年级学生体育测试情况,随机抽查了部分学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
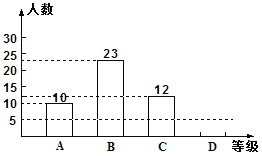
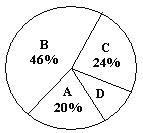
(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)请把条形统计图补充完整;
(2)样本中D级的学生人数占全班学生人数的百分比是_____________;
(3)扇形统计图中A级所在的扇形的圆心角度数是_____________;
(4)若该县九年级有8000名学生,请你用此样本估计体育测试中A级和B级的学生人数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是直角三角形
是直角三角形![]() 斜边
斜边![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),作直线
重合),作直线![]() ,分别过点
,分别过点![]() ,
,![]() 向直线
向直线![]() 作垂线,垂足分别为
作垂线,垂足分别为![]() ,
,![]() ,
,![]() 为斜边
为斜边![]() 的中点.
的中点.
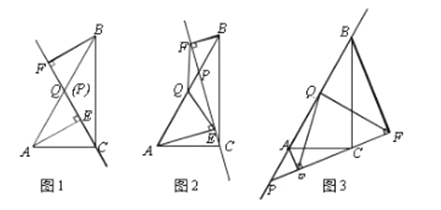
(1)如图1,当点![]() 与点
与点![]() 重合时,
重合时,![]() 与
与![]() 的位置关系是______,
的位置关系是______,![]() 与
与![]() 的数量关系是______;
的数量关系是______;
(2)如图2,当点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() 重合)时,试猜想
重合)时,试猜想![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上时,此时(2)中的结论是否仍成立?请说明理由.
的延长线上时,此时(2)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一直角三角板![]() 的直角顶点
的直角顶点![]() 在直线
在直线![]() 上,作射线
上,作射线![]() 三角板的各边和射线
三角板的各边和射线![]() 都处于直线
都处于直线![]() 的上方.
的上方.
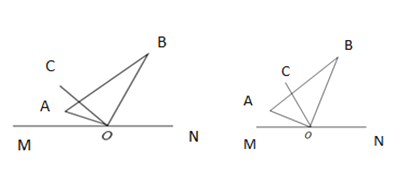
(1)将三角板绕![]() 点在平面内旋转,当
点在平面内旋转,当![]() 平分
平分![]() 时,如图1,如果
时,如图1,如果![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,将三角板![]() 绕
绕![]() 点在平面内任意转动,如果
点在平面内任意转动,如果![]() 始终在
始终在![]() 内,且
内,且![]() ,请问:
,请问:![]() 和
和![]() 有怎样的数量关系?
有怎样的数量关系?
(3)如图2,如果![]() 平分
平分![]() ,
,![]() 是否也平分
是否也平分![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列四项调查中,方式正确的是![]()
![]()
A. 了解本市中学生每天学习所用的时间,采用全面调查的方式
B. 为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式
C. 了解某市每天的流动人口数,采用全面调查的方式
D. 了解全市中学生的视力情况,采用抽样调查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:
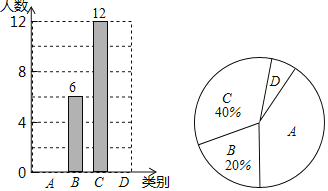
请依据统计结果回答下列问题:
(1)本次调查中,一共调查了 位好友.
(2)已知A类好友人数是D类好友人数的5倍.
①请补全条形图;
②扇形图中,“A”对应扇形的圆心角为 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,将两个完全相同的三角形纸片 ABC 和 DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)如图2,固定△ABC,使△DEC 绕点 C 旋转,当点 D 恰好落 在 AB 边上时,
①填空:线段 DE 与 AC 的位置关系是 ;
②设△BDC 的面积为 S1,△AEC 的面积为 S2,求证:S1=S2

(2)当△DEC 绕点 C 旋转到如图 3 所示的位置时,小明猜想(1) 中 S1 与 S2 的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE 边上的高,请你证明小明的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
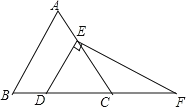
【题目】在等边三角形ABC中,点D、E分别在边BC、AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=4,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com