
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>b>a |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2+a}{{-4-4a-{a^2}}}$ | B. | $\frac{a-b}{b-a}$ | C. | $\frac{{{x^2}-4}}{x-2}$ | D. | $\frac{{{x^2}+{y^2}}}{x+y}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
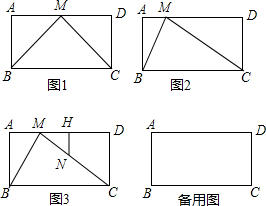
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | -$\frac{3}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
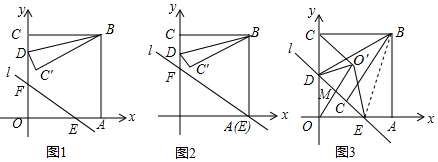
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
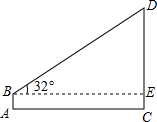 在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com