
 如图,在热气球上A处测得一栋大楼顶部B的俯角为23°,测得这栋大楼底部C的俯角为45°.已知热气球A处距地面的高度为180m,求这栋大楼的高度(精确到1m).(参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42)
如图,在热气球上A处测得一栋大楼顶部B的俯角为23°,测得这栋大楼底部C的俯角为45°.已知热气球A处距地面的高度为180m,求这栋大楼的高度(精确到1m).(参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42) 分析 首先过点A作直线BC的垂线,垂足为点D,进而求出CD的长,利用tan23°=$\frac{BD}{AD}$,得BD的长,即可得出答案.
解答 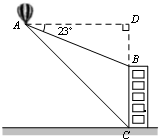 解:过点A作直线BC的垂线,垂足为点D.
解:过点A作直线BC的垂线,垂足为点D.
由题意,得∠CAD=45°,∠BAD=23°,CD=180.
∴∠CAD=∠ACD=45°.
∴CD=AD=180.
在Rt△ABD中,∠BDA=90°,$tan∠BAD=\frac{BD}{AD}=0.42$.
∴BD=0.42×180=75.6.
∴BC=CD-BD=180-75.6=104.4≈104m.
答:这栋大楼的高约为104m.
点评 此题主要考查了解直角三角形的应用,根据题意正确构造直角三角形是解题关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
| 笔试 | 面试 | 体能 | |
| 甲 | 84 | 78 | 90 |
| 乙 | 85 | 80 | 75 |
| 丙 | 80 | 90 | 73 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
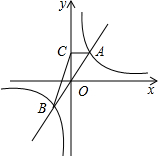 如图,正比例函数y1=mx(m>0)的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于点A(n,4)和点B,AC⊥y轴,垂足为M,△ACB的面积为8.
如图,正比例函数y1=mx(m>0)的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于点A(n,4)和点B,AC⊥y轴,垂足为M,△ACB的面积为8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com