
 13、一艘轮船从A港出发,沿着北偏东63°的方向航行,行驶至B处时发现前方有暗礁,所以转向北偏西27°方向航行,到达C后需要把航向恢复到出发时的航向,此时轮船航行的航向向顺时针方向转过的度数为( )
13、一艘轮船从A港出发,沿着北偏东63°的方向航行,行驶至B处时发现前方有暗礁,所以转向北偏西27°方向航行,到达C后需要把航向恢复到出发时的航向,此时轮船航行的航向向顺时针方向转过的度数为( ) 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
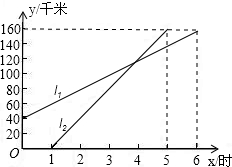 两船行驶的路程和时间的关系(其中快艇的速度大于轮船的速度).根据图象回答下列问题:
两船行驶的路程和时间的关系(其中快艇的速度大于轮船的速度).根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
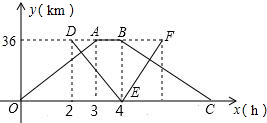 甲、乙两个港口相距36千米,一艘轮船从甲港出发,顺流航行3小时到达乙港.休息1小时后立即返回;一艘快艇在轮船出发2小时后从乙港出发,逆流航行2小时到达甲港,并立即返回(掉头时间忽略不计).已知水流的速度是1千米/米.如图表示轮船和快艇距甲港的距离y(千米)与轮船出发时间x(小时)之间的函数关系图象.
甲、乙两个港口相距36千米,一艘轮船从甲港出发,顺流航行3小时到达乙港.休息1小时后立即返回;一艘快艇在轮船出发2小时后从乙港出发,逆流航行2小时到达甲港,并立即返回(掉头时间忽略不计).已知水流的速度是1千米/米.如图表示轮船和快艇距甲港的距离y(千米)与轮船出发时间x(小时)之间的函数关系图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com