
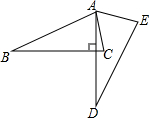
 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若AD⊥BC,∠CAE=65°,∠E=70°,则∠BAC的大小为85度.
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若AD⊥BC,∠CAE=65°,∠E=70°,则∠BAC的大小为85度. 分析 先根据旋转的性质得∠C=∠E=70°,∠BAC=∠DAE,再根据垂直的定义得∠AFC=90°,则利用互余计算出∠CAF=90°-∠C=20°,所以∠DAE=∠CAF+∠EAC=85°,于是得到∠BAC=85°.
解答 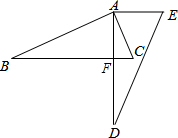 解:∵△ABC绕点A逆时针旋转得到△ADE,
解:∵△ABC绕点A逆时针旋转得到△ADE,
∴∠C=∠E=70°,∠BAC=∠DAE,
∵AD⊥BC,
∴∠AFC=90°,
∴∠CAF=90°-∠C=90°-70°=20°,
∴∠DAE=∠CAF+∠EAC=20°+65°=85°,
∴∠BAC=∠DAE=85°.
故答案为:85.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线的夹角等于旋转角.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{18}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{30}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
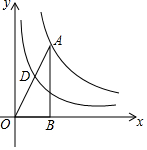 如图,已知点A在双曲线y=$\frac{8}{x}$上,AB⊥x轴于点B,连接OA交双曲线y=$\frac{k}{x}$于点D,若OD=AD,则k的值为2.
如图,已知点A在双曲线y=$\frac{8}{x}$上,AB⊥x轴于点B,连接OA交双曲线y=$\frac{k}{x}$于点D,若OD=AD,则k的值为2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
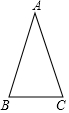 如图,△ABC中,AB=AC,∠A=36°,D为AC边上一点,将△CBD沿直线BD翻折,使翻折后的点C恰好仍在AC边上,∠CBD的度数是18°.
如图,△ABC中,AB=AC,∠A=36°,D为AC边上一点,将△CBD沿直线BD翻折,使翻折后的点C恰好仍在AC边上,∠CBD的度数是18°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)(-a-b) | B. | (a+b)(-a+b) | C. | (-a+b)(a-b) | D. | (-a+b)(b-a) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8×108 | B. | 8×109 | C. | 0.8×109 | D. | 0.8×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
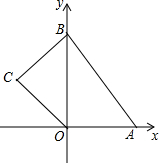 如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A的坐标为(6,0),点B的坐标为(0,8),点C的坐标为(-2$\sqrt{5}$,4),点M,N分别为四边形OABC边上的动点,动点M从点O开始,以每秒1个单位长度的速度沿O→A→B路线向中点B匀速运动,动点N从O点开始,以每秒两个单位长度的速度沿O→C→B→A路线向终点A匀速运动,点M,N同时从O点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间t秒(t>0),△OMN的面积为S.
如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A的坐标为(6,0),点B的坐标为(0,8),点C的坐标为(-2$\sqrt{5}$,4),点M,N分别为四边形OABC边上的动点,动点M从点O开始,以每秒1个单位长度的速度沿O→A→B路线向中点B匀速运动,动点N从O点开始,以每秒两个单位长度的速度沿O→C→B→A路线向终点A匀速运动,点M,N同时从O点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间t秒(t>0),△OMN的面积为S.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com