
分析 (1)将左右两式分别平方,然后比较大小;
(2)将左右两式分别加上$\sqrt{13}$,然后平方比较大小.
解答 解:(1)左式平方得,($\sqrt{5}$+$\sqrt{11}$)2=16+2$\sqrt{55}$,
右式平方得,($\sqrt{6}$+$\sqrt{10}$)2=16+2$\sqrt{60}$,
∵$\sqrt{55}$<$\sqrt{60}$,
∴16+2$\sqrt{55}$<16+2$\sqrt{60}$,
即$\sqrt{5}$+$\sqrt{11}$<$\sqrt{6}$+$\sqrt{10}$;
(2)左式加上$\sqrt{13}$,然后平方得,(2$\sqrt{13}$-$\sqrt{12}$)2=64-8$\sqrt{39}$,
右式加上$\sqrt{13}$,然后平方得,($\sqrt{14}$)2=14,
左式减去右式得:64-8$\sqrt{39}$-14=50-8$\sqrt{39}$=$\sqrt{2500}$-$\sqrt{3276}$<0,
∴左式小于右式,
即$\sqrt{13}$-$\sqrt{12}$<$\sqrt{14}$-$\sqrt{13}$.
故答案为:<;<.
点评 本题考查了实数的大小比较,比较方法往往不止一种,在比较之前先仔细观察,不要盲目下手.


科目:初中数学 来源: 题型:解答题
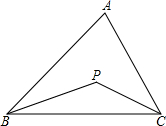 如图,在△ABC中,角平分线BP与CP相交于点P.
如图,在△ABC中,角平分线BP与CP相交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
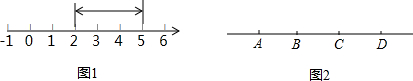
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
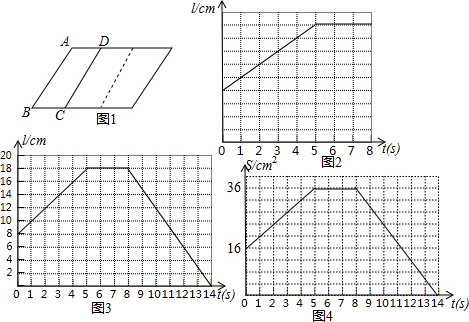
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com