
分析 (1)先把(1,m)代入y=2x-3可求出m,得到交点坐标为(1,-1),然后把(1,-1)代入y=$\frac{1}{2}$ax2可求出a的值;然后根据二次函数的性质求解;
(2)把直线与抛物线的交点问题转化为方程的问题解决:通过解方程-x2=2x-3判断有没有其他交点.
解答 解:(1)把(1,m,)代入y=2x-3得2-3=m,解得m=-1,
把(1,-1)代入y=$\frac{1}{2}$ax2,解得a=-2;
抛物线的解析式为y=-x2,对称轴为y轴;当x<0时,y随x的增大而增大;
(2)有.
理由:-x2=2x-3
解得:x1=1,x2=-3,
当x=-3时,y=-9,
此抛物线与直线还有另外的交点为(-3,-9).
点评 此题考查二次函数的性质,掌握待定系数法求函数解析式以及二次函数与一元二次方程的关系是解决问题的关键.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
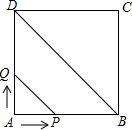 如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C移动.设运动时间为x s,由点P、B、D、Q确定的图形的面积为y cm2,求y与x(0≤x≤8)之间的函数关系式.
如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C移动.设运动时间为x s,由点P、B、D、Q确定的图形的面积为y cm2,求y与x(0≤x≤8)之间的函数关系式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在小路DF的右侧是一片草地,紧靠小路建有一正方形小屋ABCD,现用一根长为6m的牛绳一端系住牛鼻,另一端系在A处.如果小屋的边长为3m,那么这头牛最多能吃掉多大面积的草地?请画出示意图.如果绳长为7m呢?
如图,在小路DF的右侧是一片草地,紧靠小路建有一正方形小屋ABCD,现用一根长为6m的牛绳一端系住牛鼻,另一端系在A处.如果小屋的边长为3m,那么这头牛最多能吃掉多大面积的草地?请画出示意图.如果绳长为7m呢?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com