
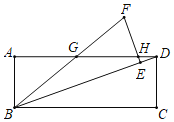
【题目】如图,矩形ABCD中,将△BCD绕点B逆时针旋转得△BEF,其中点C的对应点E恰好落在BD上.BF,EF分别交边AD于点G,H.若GH=4HD,则cos∠DBC的值为_____.
【答案】![]()
【解析】
本题求cos∠DBC的值,即求![]() ,该题思路找出与∠DBC相同的角,由旋转知∠DBC=∠FBE=∠HDE,再证明出∠F=∠GHF,设HD=x,GH=4x,BD=y,则DG=5x,则cos∠DBC=cos∠EDH,
,该题思路找出与∠DBC相同的角,由旋转知∠DBC=∠FBE=∠HDE,再证明出∠F=∠GHF,设HD=x,GH=4x,BD=y,则DG=5x,则cos∠DBC=cos∠EDH,![]() ,∴
,∴![]() ,求出
,求出![]() 即可.
即可.
解:∵将△BCD绕点B逆时针旋转得△BEF,其中点C的对应点E恰好落在BD上.
∴∠FBE=∠DBC,BF=BD,BE=BC,∠BEF=∠C=90°,
∵矩形ABCD中,AD∥BC,
∴∠EDH=∠DBC,
∴∠FBE=∠DBC=∠EDH,
∴BG=DG,
∵GH=4HD,
∴设HD=x,GH=4x,设BE=BC=y,
则BG=DG=5x,
∵∠DHE+∠EDH=90°,∠F+∠FBE=90°,∠FBE=∠EDH,
∴∠F=∠DHE,
∵∠FHG=∠DHE,
∴∠F=∠FHG,
∴GF=GH=4x,
∴BF=BD=9x,DE=9x﹣y,
∵cos∠DBC=cos∠EDH,
∴![]() ,
,
∴![]() ,
,
∴xy=81x2﹣9xy,
∴10xy=81x2,
∴10y=81x,
∴![]() ,,即cos∠DBC=
,,即cos∠DBC=![]() .
.
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
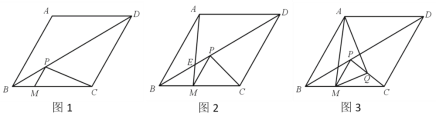
【题目】已知菱形ABCD中,∠ABC=60°,AB=4,点M在BC边上,过点M作PM∥AB交对角线BD于点P,连接PC.
(1)如图1,当BM=1时,求PC的长;
(2)如图2,设AM与BD交于点E,当∠PCM=45°时,求证:![]() =
=![]() ;
;
(3)如图3,取PC的中点Q,连接MQ,AQ.
①请探究AQ和MQ之间的数量关系,并写出探究过程;
②△AMQ的面积有最小值吗?如果有,请直接写出这个最小值;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深入开展校园阳光一小时活动,九年级(1)班学生积极参与锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行锻炼,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图:
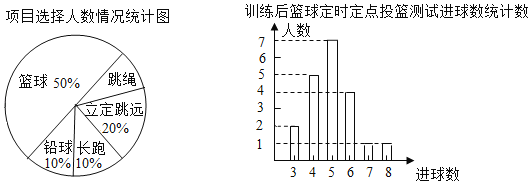
请你根据上面提供的信息回答下列问题:
(1)(扇形图中)跳绳部分的扇形圆心角为 度,该班共有 人;训练后,篮球定时定点投篮每个人进球数的平均数是 ,众数是 ;
(2)老师决定从选择跳绳训练的3名女生和1名男生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
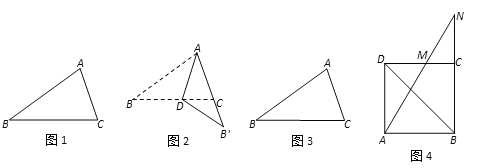
【题目】阅读材料:等腰三角形具有性质“等边对等角”.事实上,不等边三角形也具有类似性质“大边对大角”:如图1.在△ABC中,如果AB>AC,那么∠ACB>∠ABC.证明如下:将AB沿△ABC的角平分线AD翻折(如图2),因为AB>AC,所以点B落在AC的延长线上的点B'处.于是,由∠ACB>∠B',∠ABC=∠B',可得∠ACB>∠ABC.
(1)灵活运用:从上面的证法可以看出,折纸常常能为证明一个命题提供思路和方法.由此小明想到可用类似方法证明“大角对大边”:如图3.在△ABC中,如果∠ACB>∠ABC,那么AB>AC.小明的思路是:沿BC的垂直平分线翻折……请你帮助小明完成后面的证明过程.
(2)拓展延伸:请运用上述方法或结论解决如下问题:
如图4,已知M为正方形ABCD的边CD上一点(不含端点),连接AM并延长,交BC的延长线于点N.求证:AM+AN>2BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC中,点D,E分别为直角边AC,BC上的点,若满足AD2+BE2=DE2,则称DE为R△ABC的“完美分割线”.显然,当DE为△ABC的中位线时,DE是△ABC的一条完美分割线.
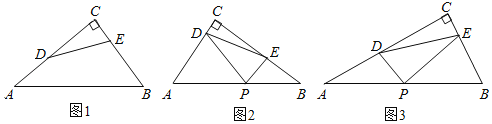
(1)如图1,AB=10,cosA=![]() ,AD=3,若DE为完美分割线,则BE的长是 .
,AD=3,若DE为完美分割线,则BE的长是 .
(2)如图2,对AC边上的点D,在Rt△ABC中的斜边AB上取点P,使得DP=DA,过点P画PE⊥PD交BC于点E,连结DE,求证:DE是直角△ABC的完美分割线.
(3)如图3,在Rt△ABC中,AC=10,BC=5,DE是其完美分割线,点P是斜边AB的中点,连结PD、PE,求cos∠PDE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由边长为1个单位长度的小正方形组成的网格图中有格点△ABC(注:顶点在网格线交点处的三角形叫做格点三角形).只用没有刻度的直尺,按如下要求画图,
(1)以点C为位似中心,在如图中作△DEC∽ABC,且相似比为1:2;
(2)若点B为原点,点C(4,0),请在如图中画出平面直角坐标系,作出△ABC的外心,并直接写出△ABC的外心的坐标
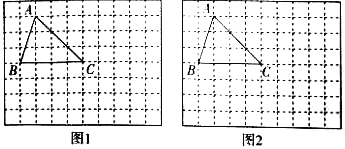
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】调查作业:了解你所住小区家庭3月份用气量情况.
小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2—5之间,这300户家庭的平均人数约为3.3.
小天、小东和小芸各自对该小区家庭3月份用气量情况进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2、表3,
表1抽样调查小区4户家庭3月份用气量统计表(单位:![]() )
)
家庭人数 | 2 | 3 | 4 | 5 |
用气量 | 14 | 19 | 21 | 26 |
表2抽样调查小区15户家庭3月份用气量统计表(单位:![]() )
)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
用气量 | 10 | 11 | 15 | 13 | 14 | 15 | 17 | 17 | 18 | 18 | 18 | 18 | 18 | 20 | 22 |
表3抽样调查小区15户家庭3月份用气量统计表(单位:![]() )
)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
用气量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 20 | 20 | 21 | 22 | 26 | 31 | 28 | 31 |
根据以上材料回答问题:
(1)小天、小东和小芸三人中,哪一位同学抽样调查的数据能较好地反应出该小区家庭3月份用气量情况?请简要说明其他两位同学抽样调查的不足之处;
(2)小东将表2中的数据按用气量![]() 大小分为三类;
大小分为三类;
①节约型:![]() ;
;
②居中型:![]() ;
;
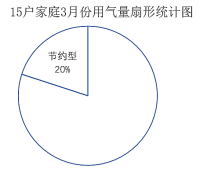
③偏高型:![]() ;并绘制成如下扇形统计图,请帮助他将扇形图补充完整;
;并绘制成如下扇形统计图,请帮助他将扇形图补充完整;
(3)小芸算出表3中3月份平均每人的用量为![]() ,请估计该小区3月份的总用气量.
,请估计该小区3月份的总用气量.
查看答案和解析>>
科目:初中数学 来源: 题型:
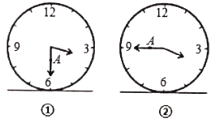
【题目】图①表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10cm.图②表示当钟面显示3点45分时,A点距桌面的高度为16cm,若钟面显示3点55分时,A点距桌面的高度为____![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com