
【题目】下列不等式变形,成立的是( )
A.若m<n,则m-2<n-2B.若m<n,则2-m<2-n
C.若m<n,则-2m<-2nD.若m<n,则![]()
科目:初中数学 来源: 题型:
【题目】如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
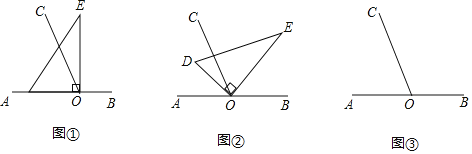
(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE °.
(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,则∠COD= °.
(3)如图③,将直角三角板DOE绕点O顺时针方向转动到某个位置,0°<∠AOD<180°,如果∠COD=![]() ∠AOE,求∠COD的度数.
∠AOE,求∠COD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
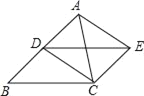
【题目】 已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形.
(1)求证:四边形ADCE是平行四边形;
(2)在△ABC中,若AC=BC,则四边形ADCE是 ;(只写结论,不需证明)
(3)在(2)的条件下,当AC⊥BC时,求证:四边形ADCE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个教师承担本学期期末考试的第17题的网上阅卷任务,若由这三人中的某一人独立完成阅卷任务,则甲需要15小时,乙需要10小时,丙需要8小时。
(1)如果甲、乙、丙三人同时改卷,那么需要多少时间完成?
(2)如果按照甲、乙、丙、甲、乙、丙、……的次序轮流阅卷,每一轮中每人各阅卷1小时。那么要多少小时完成?
(3)能否把(2)题所说的甲、乙、丙的次序作适当调整,其余的不变,使得完成这项任务的时间至少提前半小时?(答题要求:如认为不能,需要说明理由;如认为能,请至少说出一种轮流的次序,并求出相应能提前多少时间完成阅卷任务)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D,E是△ABC中AB,BC边上的点,且DE∥AC,∠ACB角平分线和它的外角的平分线分别交DE于点G和H.则下列结论错误的是( )

A. 若BG∥CH,则四边形BHCG为矩形
B. 若BE=CE时,四边形BHCG为矩形
C. 若HE=CE,则四边形BHCG为平行四边形
D. 若CH=3,CG=4,则CE=2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】)图①中是一座钢管混凝土系杆拱桥,桥的拱肋ACB可视为抛物线的一部分(如图②),桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,测得拱肋
的跨度AB为200米,与AB中点O相距20米处有一高度为48米的系杆.
【1】求正中间系杆OC的长度;
【2】若相邻系杆之间的间距均为5米(不考虑系杆的粗细),则是否存在一根系杆的长度恰好是OC长度的一半?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017贵州省遵义市)如图,抛物线![]() (a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为
(a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为![]() .
.
(1)求该抛物线的函数关系式与C点坐标;
(2)已知点M(m,0)是线段OA上的一个动点,过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,当m为何值时,△BDE恰好是以DE为底边的等腰三角形?
(3)在(2)问条件下,当△BDE恰好是以DE为底边的等腰三角形时,动点M相应位置记为点M′,将OM′绕原点O顺时针旋转得到ON(旋转角在0°到90°之间);
①探究:线段OB上是否存在定点P(P不与O、B重合),无论ON如何旋转,![]() 始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;
始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;
②试求出此旋转过程中,(NA+![]() NB)的最小值.
NB)的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知开口向上的抛物线y=ax2+bx+c,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc>0;③a-2b+4c<0;④8a+c>0.其中正确的有
A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com