
 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:解答题
 为推进多城同创,打造宜业宜居家园,温岭市交通部门一再提醒司机:为了安全,请勿超速,并进一步完善各类监测系统,如图,在泽太一级公路某直线路段MN内限速80千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了4秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
为推进多城同创,打造宜业宜居家园,温岭市交通部门一再提醒司机:为了安全,请勿超速,并进一步完善各类监测系统,如图,在泽太一级公路某直线路段MN内限速80千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了4秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
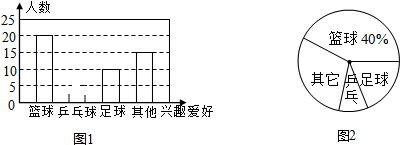
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
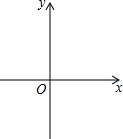 已知抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D.
已知抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 径赛项目 | 800m,200m(分别用A1,A2表示) |
| 田赛项目 | 跳远,跳高,掷实心球(分别用B2,B3表示) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 从现在起经过I3至14年F市将会发生一次地震 | |
| B. | 可以确定F市在未来20年内将会发生一次地震 | |
| C. | 未来20年内,F市发生地震的可能性比没有发生地震的可能性大 | |
| D. | 我们不能判断未来会发生什么事,因此没有人可以确定何时会有地震发生 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com