
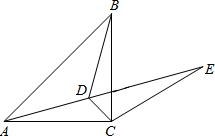
 如图所示,已知点D为等腰直角三角形ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA,则∠DCE的度数是105°.
如图所示,已知点D为等腰直角三角形ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA,则∠DCE的度数是105°. 分析 根据等腰直角△ABC,求出CD是边AB的垂直平分线,求出CD平分∠ACB,根据CE=CA,∠CAD=15°,求出∠ACE=150°即可利用角的和差求解.
解答 解:∵△ABC是等腰直角三角形,
∴∠BAC=∠ABC=45°,
∵∠CAD=∠CBD=15°,
∴∠BAD=∠ABD=45°-15°=30°,∠ABD=∠ABC-15°=30°,
∴BD=AD,
∴D在AB的垂直平分线上,
∵AC=BC,
∴C也在AB的垂直平分线上,
即直线CD是AB的垂直平分线,
∴∠ACD=∠BCD=45°,
∵∠CAD=15°,CE=CA,
∴∠CED=∠CAD=15°,
∴∠ECA=150°,
∴∠DCE=∠ECA-∠ACD=150°-45°=105°.
故答案为:105°.
点评 此题主要考查等腰直角三角形,线段垂直平分线的性质与判定、等腰三角形的性质等知识点,难易程度适中,是一道很典型的题目.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{{({-2})}^2}}$等于-2 | B. | ±$\sqrt{9}$等于3 | ||
| C. | ﹙-5﹚3的立方根是5 | D. | $\sqrt{16}$平方根是±2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
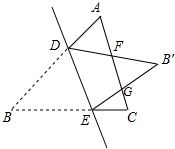 已知△ABC中,AC=BC,点D、E分别在边AB、AC上,把△BDE沿直线DE翻折,使点B落在B′处,DB′,EB′分别交AC于点F、G,若∠ADF=80°,则∠EGC的大小为( )
已知△ABC中,AC=BC,点D、E分别在边AB、AC上,把△BDE沿直线DE翻折,使点B落在B′处,DB′,EB′分别交AC于点F、G,若∠ADF=80°,则∠EGC的大小为( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com